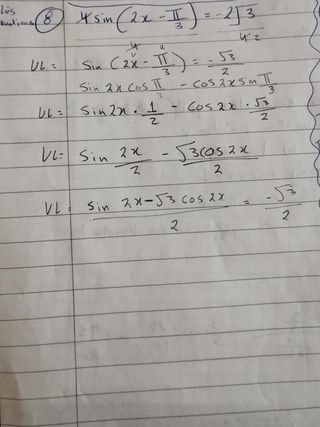Ekvation

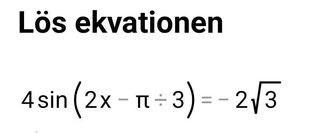
Dividera båda led med 4. Sätt därefter t=2x-pi/3. Då får du en ekv. på formen sin t = a, där -1<=a<=1 som du löst många gånger tidigare.

Alltså: 

sin (2x - pii/3) = - $\sqrt{}$3 /2

Ja

Hoppsan, här blev det lite tokigt i tredje sista raden. 1/2 är en faktor utanför sin. Du behöver inte an-vända summaformeln för sin. Ta bara sin t= -$\sqrt{3}$/2 som ger t₁=  4 pi/3 +2 pi* n och t₂ = 5 pi/3+2 pi* n  och sätt sedan tillbaka t=2x-pi/3 för att bestämma x-värdena.

Tomten skrev:

Hoppsan, här blev det lite tokigt i tredje sista raden. 1/2 är en faktor utanför sin. Du behöver inte an-vända summaformeln för sin. Ta bara sin t= -$\sqrt{3}$/2 som ger t₁=  4 pi/3 +2 pi* n och t₂ = 5 pi/3+2 pi* n  och sätt sedan tillbaka t=2x-pi/3 för att bestämma x-värdena.

tjena, försökte också lösa för skojsskull, fick

$\begin{array}{l}{x}_1=\frac{2}{3}\pi +\pi k,k\in \mathrm{ℝ}\\ x_2=\frac{5}{6}\pi +\pi k,k\in \mathrm{ℝ}\end{array}$ verkar dock inte stämma överens med wolfram som säger $\begin{array}{l}x=\pi k,k\in \mathrm{ℝ}\\ x=-\frac{\pi }{6}+\pi k,k\in \mathrm{ℝ}\end{array}$

stämmer din lösning överens med min?

Jajamensan, (Jag skrev dock inte -pi/6 utan 5pi/6, men det är samma vinkel). Ett fel ser jag: Du har  skrivit  k tillhör R och det stämmer inte. k kan t ex inte vara 1/2 utan får bara vara ett HELTAL. k ska alltså tillhöra Z.

Jag läste nog fel. Är de två sista raderna Wolfram och raderna ovanför din lösning? I så fall är det Wolfram som stämmer med min lösning utom betr. talområdet för k, för där har Wolfram fel. Skulle k kunna vara vilket reellt tal som helst så skulle alla reella tal kunna göras till lösningar till ekv.