Ekvation z^n
Jag förstår inte riktigt hur jag ska göra.. i facit står det att r^3=27 och r=3. Det förstår jag. Men jag förstår inte hur de får 3v=270+n•360
Uppgift b.

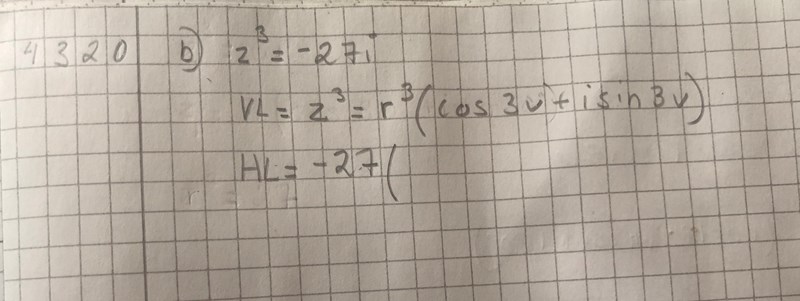
Man måste ha med periodiciteten för sin och cosfunktionerna, så här:
z3 = -27i
Beloppet z = 3, det är du med på, argumentet z3 är 3pi/2 då får vi
z3 = 33(cos(3pi/2 + 2npi) + isin(3pi/2 + 2npi)) Där n kan anta värdena 0, 1 eller 2
Sen drar vi tredjeroten ur beloppet och delar argumenten med 3
z = 3(cos((3pi/2 + 2npi)/3) + isin((3pi/2 + 2npi)/3)) Där n kan anta värdena 0, 1 eller 2
och förenklar
z = 3(cos((pi/2 + 2/3npi)) + isin((pi/2 + 2/3npi))) Där n kan anta värdena 0, 1 eller 2
z1 = 3(cos(pi/2)+isin(pi/2)), gäller för n = 0
bestäm sen vad cos och sin antar för värden och du är klar med z1
n = 1 och n = 2 får du göra själv
Ture skrev:Man måste ha med periodiciteten för sin och cosfunktionerna, så här:
z3 = -27i
Beloppet z = 3, det är du med på, argumentet z3 är 3pi/2 då får vi
z3 = 33(cos(3pi/2 + 2npi) + isin(3pi/2 + 2npi)) Där n kan anta värdena 0, 1 eller 2
Sen drar vi tredjeroten ur beloppet och delar argumenten med 3
z = 3(cos((3pi/2 + 2npi)/3) + isin((3pi/2 + 2npi)/3)) Där n kan anta värdena 0, 1 eller 2
och förenklar
z = 3(cos((pi/2 + 2/3npi)) + isin((pi/2 + 2/3npi))) Där n kan anta värdena 0, 1 eller 2
z1 = 3(cos(pi/2)+isin(pi/2)), gäller för n = 0
bestäm sen vad cos och sin antar för värden och du är klar med z1
n = 1 och n = 2 får du göra själv
jag förstår inte hur du får fram argumentet.. och jag vet inte hur jag ska rita upp det
Argumentet för - 27i får du fram genom att rita in talet i ett koordinatsystem
Det ligger på negativa imagimära axeln.
Ture skrev:Argumentet för - 27i får du fram genom att rita in talet i ett koordinatsystem
Det ligger på negativa imagimära axeln.
är det därför det blir 270 grader?
Just det, om du vrider moturs (positiv ritning i matematiken) från positiva reella axeln till negativa imaginära axeln så har du vridit 3*90 = 270 grader eller 3pi/2 radianer


