Ekvationen med konjugaterna
Försöker lösa ut följande uppgiften: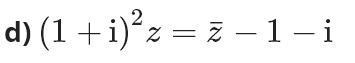
Allt jag får är :
2i(x+yi)-(x-yi)=-1-i
Problemet blir när jag försöker sammla ut termerna för x och y ur
x+yi=(1+xi+y+i)/-2
Xet innehåller i, men hur gör jag mig av med den? Kanske jag sammlar termerna på ett fel sätt
Hej!
Eftersom vissa termer innehåller och uttrycket betyder att de reella talen utan "" representeras av x , medans de termer som har som faktor, representeras av y.
Du krånglar till det en del. Det räcker att du skriver det på formen:
Sedan fås:
samt
DreamChild skrev:Försöker lösa ut följande uppgiften:
Allt jag får är :
2i(x+yi)-(x-yi)=-1-i
Problemet blir när jag försöker sammla ut termerna för x och y ur
x+yi=(1+xi+y+i)/-2
Xet innehåller i, men hur gör jag mig av med den? Kanske jag sammlar termerna på ett fel sätt
2i(x + yi) - (x - yi) = -1 - i
2xi - 2y - x + yi = -1 - i
-(x + 2y) + (2x + y)i = -1 - i
Följ nu rådet från tomast80 och identifiera real- respektive imaginärdelarna i VL och HL.



