Ekvationer
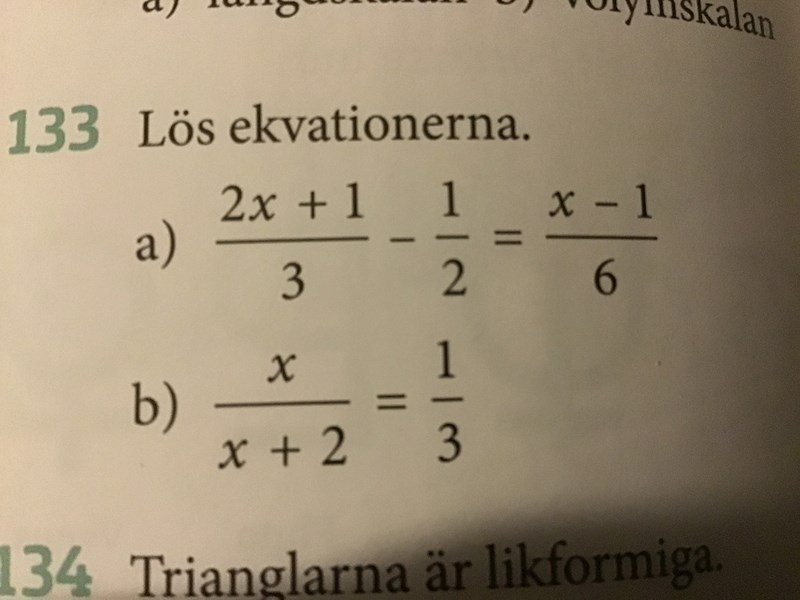
Skulle nån kunna hjälpa mig med dem. Uppskattar hjälpen.
Metoden för denna typ av ekvationer är att multiplicera alla termer med gemensam nämnare
Så att alla nämnare kan förkortas bort och du får en 'vanlig' ekvation att lösa
Behöver du mer hjälp ?
Henning skrev:Metoden för denna typ av ekvationer är att multiplicera alla termer med gemensam nämnare
Så att alla nämnare kan förkortas bort och du får en 'vanlig' ekvation att lösaBehöver du mer hjälp ?
Ja det visste jag men är fundersam på hur man får fram mgn.
Den enklaste vägen är att du bildar den som produkt av all nämnare i uppgiften
Så i a) blir den =36 - den går ju jämnt upp i alla nämnare
Däremot är den minsta gemensamma nämnaren 6
I b) blir den då
Kommer du vidare nu ?
Vad menar du med att den går upp med alla nämnare?
Jag menar: är jämnt delbart
Så att du kan förkorta bort nämnarna
Testa med det du skrev till mig men fick inte rätt svar, tror pga att jag inte vet vad jag ska göra efter det.
Jag visar i b-uppgiften
Multiplicerar alla termer med (x+2) *3
Dvs
Detta kan nu skrivas
Efter förkortning återstår
Dvs en enkel ekvation vars lösning är x=1
Henning skrev:Jag visar i b-uppgiften
Multiplicerar alla termer med (x+2) *3
Dvs
Detta kan nu skrivas
Efter förkortning återstår
Dvs en enkel ekvation vars lösning är x=1
Jaha, nu fick jag grepp på det. Tack så mycket. :)

