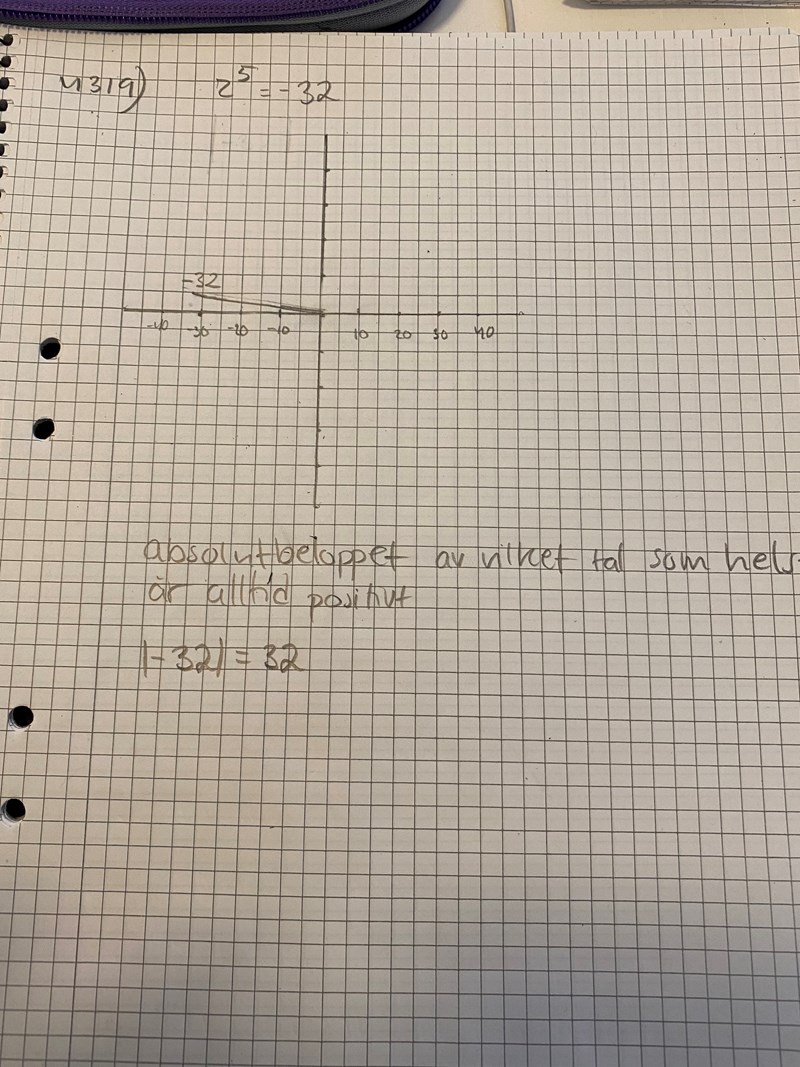ekvationer med komplexa rötter

Rita in talet -32 i det komplexa talplanen. Vilket argument har detta tal?

32?

gör jag såhär: $-32= aboslutbeloppet \left|32i\right|=\sqrt{{32}^2}=\sqrt{1024}=32$

Rita upp. Lägg upp bilden här. Sedan kan vi börja diskutera. Det du verkar tänka på är absolutbeloppet (tror jag), inte argumentet.  Argumentet skall vara en vinkel, lämpligen i radianer.

förlåt men jag förstår inte

Vi är fortfarande på a-uppgiften.

Du ska där uttrycka det komplexa talet $-32$ på polär form $w=r(\cos(v)+i\sin(v))$.

För att gör det behöver du dels ta reda på talets absolutbelopp $r$, dels talets argument $v$.

Börja då med att markera talet $-32$ i det komplexa talplanet. Rita sedan ett streck (en vektor) från origo till punkten du har markerat.

Då är talets

• absolutbelopp $r$ lika med längden av strecket, dvs avståndet från origo tlli talet.
• argument $v$ lika med vinkeln mellan den positiva reella axeln och strecket, räknat moturs.

Börja med att rita in talet -32 i det komplexa talplanet. Lägg upp bilden här. Är det klart vad du skall göra så långt?

Jag tycker att det ser ut som att du har markerat talet w = -32+5i, inte talet w = -32.

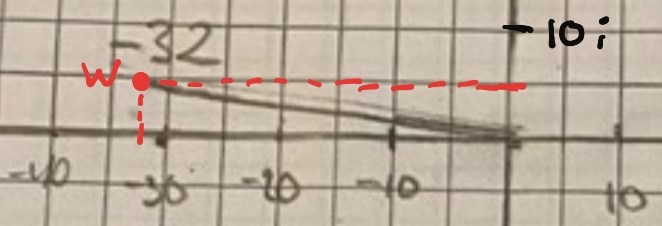
hmm okej men då ska vektorn gå rakt längs med linjen?

Ja, punkten skall ligga "på negativa x-axeln" om man tänker sig det som ett vanligt koordinatsystem.

Du kan se det komplexa talplanet som ett vanligt koordinatsystem.

Det komplexa talet a + bi markeras som punkten (a, b) i det komplexa talplanet.

Därför ska det komplexa talet -32 (vilket kan skrivas som -32 + 0i) markeras som punkten (-32, 0) i det komplexa talplanet.

Läs gärna mer om detta här och fråga om allt som är oklart.