Svara exakt - Radianer
Hej! Jag vet inte hur jag ska gå till väga för att lösa dessa 2 ekvationerna. Tacksam för lite vägledning.


Dr.scofield skrev:Hej! Jag vet inte hur jag ska gå till väga för att lösa dessa 2 ekvationerna. Tacksam för lite vägledning.
Jag tror inte det är några ekvationer, utan att du skall beräkna uttrycken exakt.
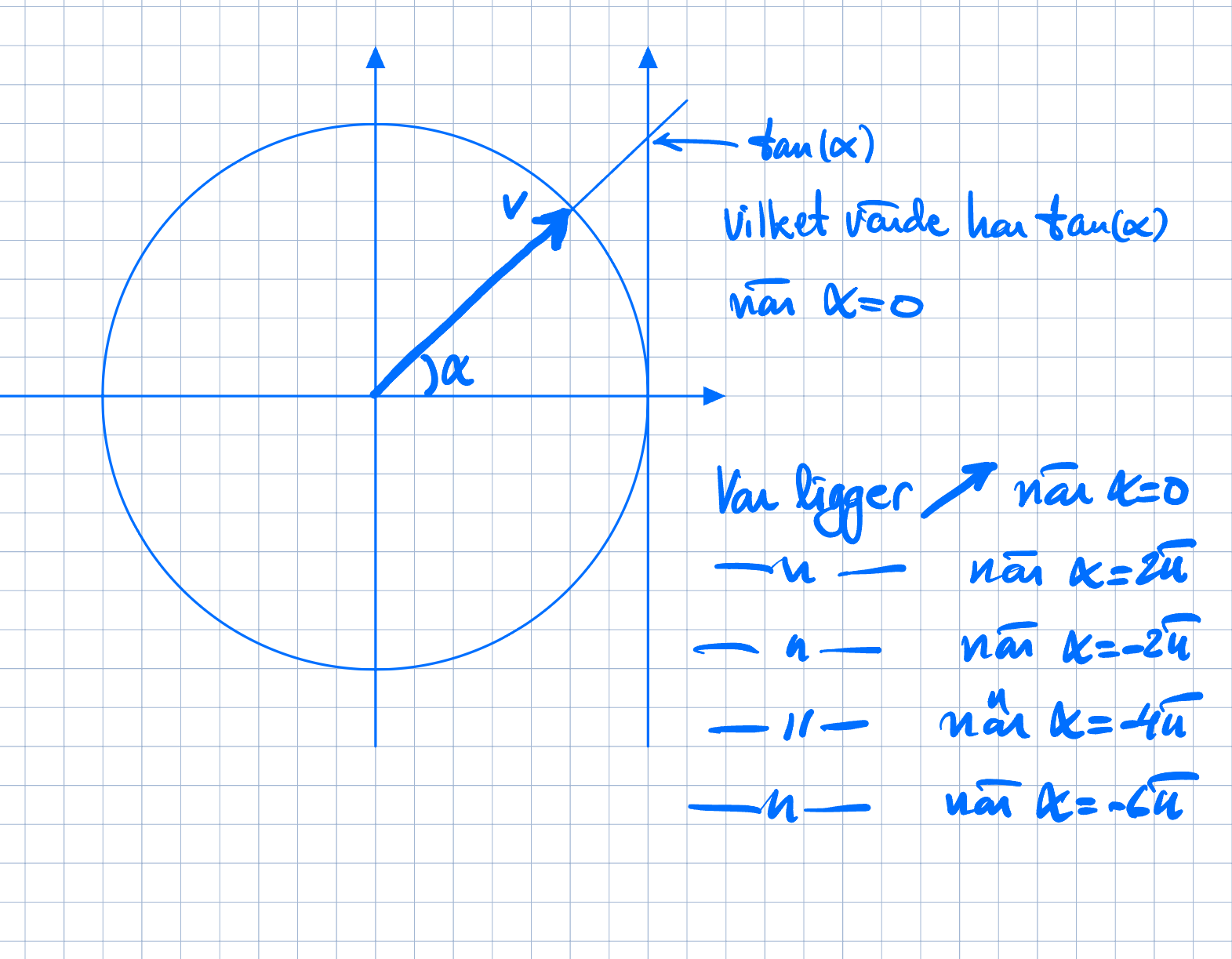
Vad är tan(0) och vad blir då tan(-6π)?
Här är det mycket viktigt att rita sin enhetscirkel. Den ger alla svaren nästan direkt.
Ge oss en ansats med bild så hjälper vi dig vidare!
Ja det stämmer, tröttheten börjar visa sig hehe.
Tan(0) = 0? Jag vet inte hur detta ska leda mig till att veta vad tan(-6pi) blir.
Dr.scofield skrev:Ja det stämmer, tröttheten börjar visa sig hehe.
Tan(0) = 0? Jag vet inte hur detta ska leda mig till att veta vad tan(-6pi) blir.
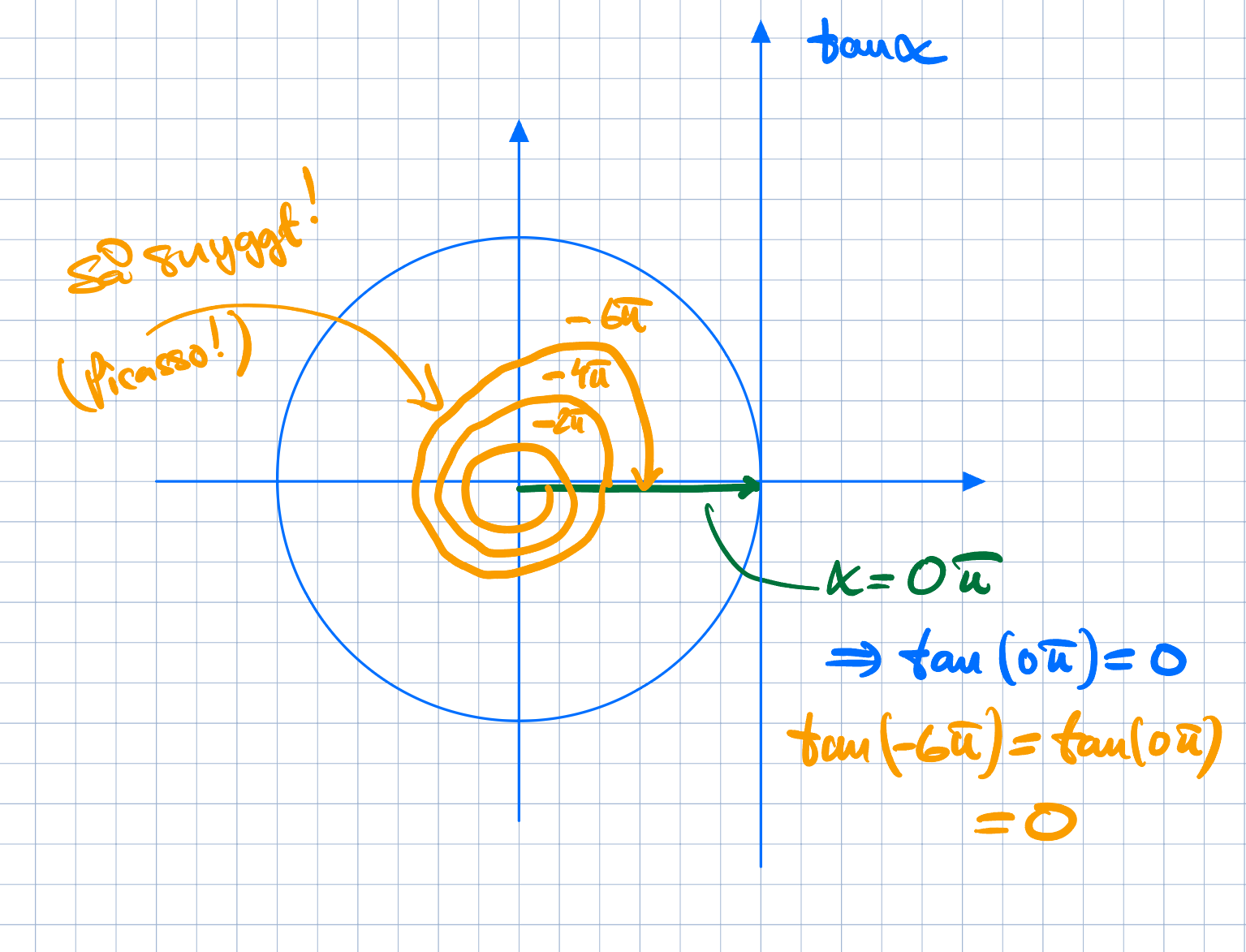
Förstår inte hur tan(-6pi) ockå är lika med 0? :0 Jämna tal * pi verkar vara = 0, eller kanske är jag helt ute och cyklar.
Dr.scofield skrev:Förstår inte hur tan(-6pi) ockå är lika med 0?
Klicka här för ett annat sätt att förklara det
Är du med på att sinus- och cosinusfunktionerna är periodiska med perioden 2pi, dvs att sin(v) = sin(v+2pi) och att cos(v) = cos(v+2pi)?
Är du med på att detta kan skrivas sin(v) = sin(v+n*2pi) och cos(v) = cos(v+n*2pi), där n är ett heltal?
Detta gäller även tangensfunktionen, fast där är perioden pi.
Vi har alltså att tan(v) = tan(v+n*pi).
Ser du då att tan(0) = tan(-6pi)?
Nuuu ja! Nu hänger jag med! Det är därför det blir jämna tal också. Tack för hjälpen snälla ni!