Ekvationssystem
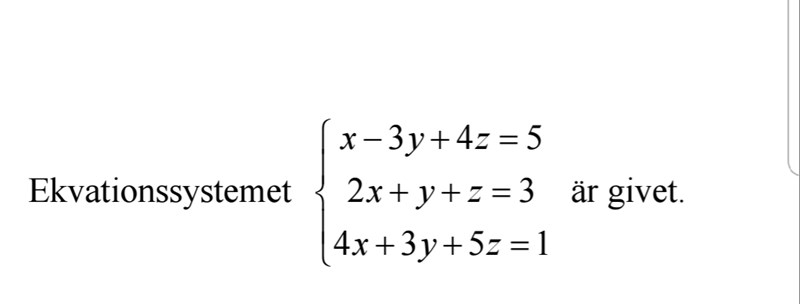 Hur kan man bestämma i förväg, utan att börja lösa ekvationensystemet, att det kommer att får n entydig lösning?
Hur kan man bestämma i förväg, utan att börja lösa ekvationensystemet, att det kommer att får n entydig lösning?
Jag vet att ekvationsystem med lika många ekvationer som obekanta har vanligtvis entydiglösning; man får ut värdet på en av de obekanta i var och en av ekvationerna. Vad menar de egentligen? Hur kan jag se det med ögat.
Jag gissar att du läst om determinanter.
Om du konstruerar en matrisekvation av det hela:
där är en -matris av koefficienterna för och kan du direkt säga att ekvationssystemet har en entydig lösning om och endast om .
Om de tre ekvationerna inte är linjärt oberoende, kommer ekvationssystemet inte att ha en entydig lösning. Ibland kan detta vara enkelt att se.
Menar du att jag kan avgöra det genom att se om matrisen är kvadratiskt samt att det(A)≠0?
Kalmar.T skrev:Menar du att jag kan avgöra det genom att se om matrisen är kvadratiskt samt att det(A)≠0?
Ja.
Ser du vad matrisen blir?
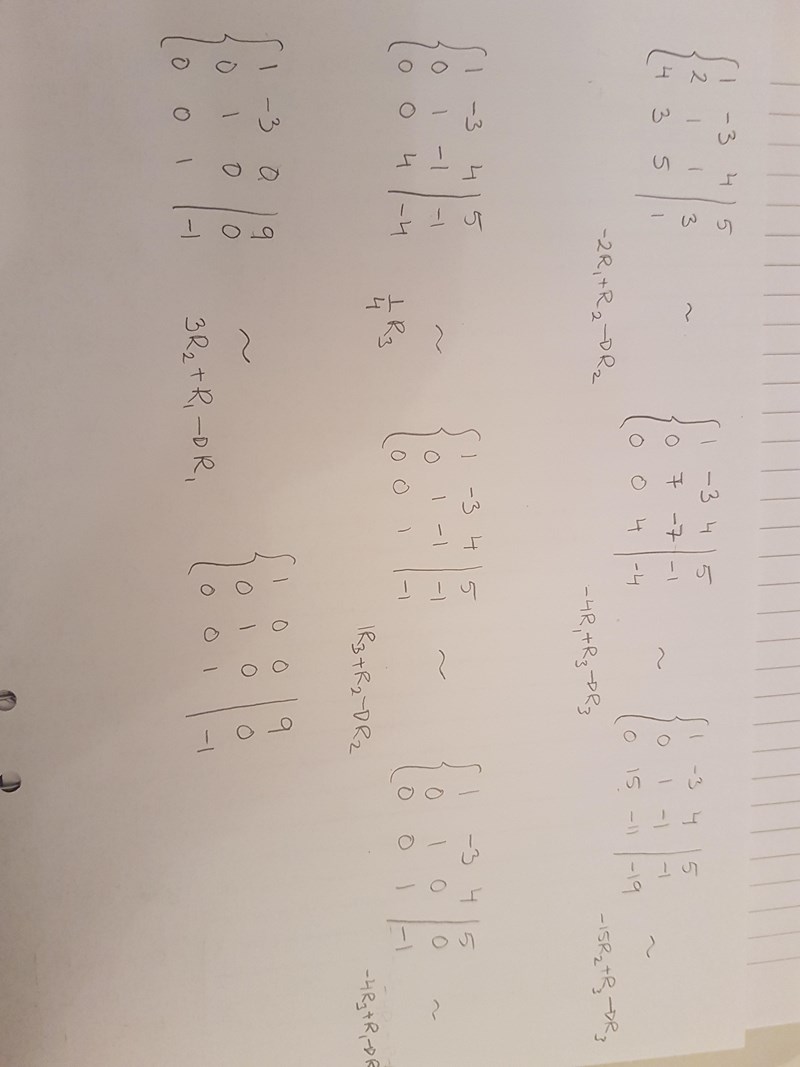 var kan jag ha gjort fel?
var kan jag ha gjort fel?
Du gör en miss på mittenraden. Du räknar som att . Det borde vara:

Om man räknar ut determinanten, har man inte gjort mer än halva jobbet med att lösa systemet då?
x = 4
y= -2
z= -1
Kalmar.T skrev:x = 4
y= -2
z= -1
Har du kontrollerat om dessa värden på de obekanta verkligen är en lösning till ekvationssystemet?
Om ja, vad fick du för resultat?
Om nej, vet du hur du i så fall skulle gå till väga?
x= 3
y= -2
z= -1
Kalmar.T skrev:x= 3
y= -2
z= -1
Har du kontrollerat om dessa värden på de obekanta verkligen är en lösning till ekvationssystemet?
Om ja, vad fick du för resultat?
Om nej, vet du hur du i så fall skulle gå till väga?
ja
Kalmar.T skrev:ja
Du är kortfattad, innebär det att du är nöjd eller vill du få reda på fler slarvfel du gjorde i ursprungsberäkningen?
du får gärna berätta om mina slarvfel
Kalmar.T skrev:du får gärna berätta om mina slarvfel
Första operationen:
- fel värde i högerledet rad 2 (rödmarkerat)
- hur kom du fram till rad 3 (blåmarkerat)?
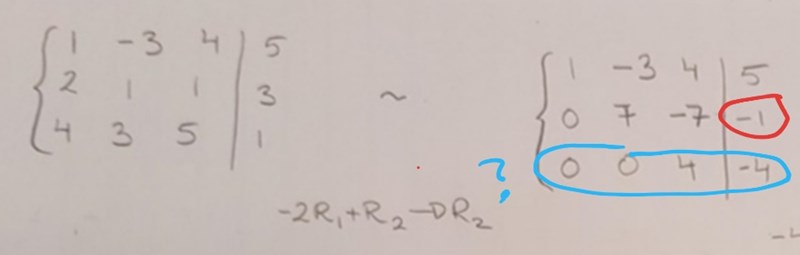
Andra operationen, rad 2:
Hur gick du från [0 7 -7 | -1] till [0 1 -1 | -1]?
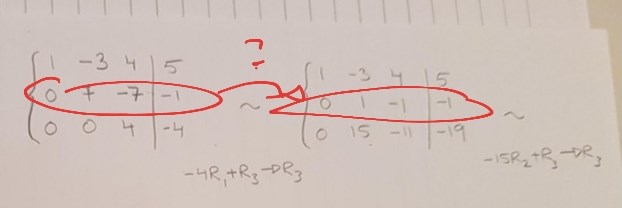
Yngve skrev:Andra operationen, rad 2:
Hur gick du från [0 7 -7 | -1] till [0 1 -1 | -1]?
Det underliga är att alla fel är tillrättade i denna högra matrisen (det slutgiltiga svaret är alltså rätt), det känns nästan som om den vänstra skrivits över med något annat.
1. Ser nu att värdet på rad två ska vara -7
2.Jag delade rad 2 med 7 och fick därför svaret (0 1 -1 | -1
Kalmar.T skrev:1. Ser nu att värdet på rad två ska vara -7
OK det stämmer
2.Jag delade rad 2 med 7 och fick därför svaret (0 1 -1 | -1
Om du delar rad 2 med 7 så måste du även dela högerledet med 7. Det skulle då bli .
-------------
Av ren nyfikenhet, hur kom du fram till rätt svar till slut?
Nej, om högerledet på rad två blev 7, och jag delade VL och HL med 7 så stämmer uträkningen på rad två.
Alltså i början var rad två ( 0 7 -7 | -7 , när jag delar HL och VL med 7, får jag ( 0 1 -1 | - 1
Som p.auto beskriver. När jag sätter in x, y och z värden i ekvationen så stämmer min lösning
Kalmar.T skrev:Som p.auto beskriver. När jag sätter in x, y och z värden i ekvationen så stämmer min lösning
Jag ifrågasätter inte att lösningen är rätt, jag är bara förundrad över hur du kom fram till rätt svar trots alla felaktigheter i uträkningarna.





