Ekvationssystem, bestäm för varje värde på a alla lösningar

Hej!

Se följande länk: https://www.pluggakuten.se/trad/linjar-algebra-ekvationssystem-bestam-for-vilka-varden-pa-parameterna-a/?#post-937abcd3-3349-4889-a186-aa0e00cb9ce8

Hej!

Skriv systemet på matrisform $AX=B.$ Beräkna determinanten $\det A$ genom att använda elementära rad-eller kolonnoperationer för att skapa så många nollor som möjligt. Utveckla sedan längs den rad eller kolonn som innehåller flest nollor.

Om $\det A \neq 0$ så har systemet den unika lösningen $X = A^{-1}B$.

Om $\det A = 0$ så kan systemet sakna lösning eller ha flera lösningar. Studera speciellt fallet då parametern $b=-6$; troligtvis kommer detta leda till att systemet saknar lösning. 

Alltså är det(A)=0 när a=0 och när a≠0 är det(A)≠0 och då är systemmatrisen inverterbar. Lösningen ges när a≠ 0 av systemmatrisen invers, dvs. $X=A^{-1}b.$

Jag ska nu beräkna inversen för att få lösningen på vad x, y och z blir när a≠0.

Jag vet att jag fårlösningen för x, y och z när det(A)≠ 0 vilket i detta fall sammanfaller med att a≠0.

Lösningen ges av $X=A^1·B=\left(\begin{array}{ccc}inversen av systemmatrisen& & \\ & & \\ & & \end{array}\right) · \left(\begin{array}{c}2\\ 4\\ b+6\end{array}\right)=\left(\begin{array}{c}\begin{array}{c}x\\ y\end{array}\\ z\end{array}\right)$.

Nu skulle jag behöva hjälp med att räkna ut inversen till systemmatrisen, jag har riktigt kört fast. Jag ska ju sakta men säkert förvandla systemmatrisen till enhetsmatrisen som bara har en diagonal av ettor och resten ska vara nollor. Jag har dock problem med arr få bort a.

Se här hur långt jag har kommit och ge mig gärna råd och tips.

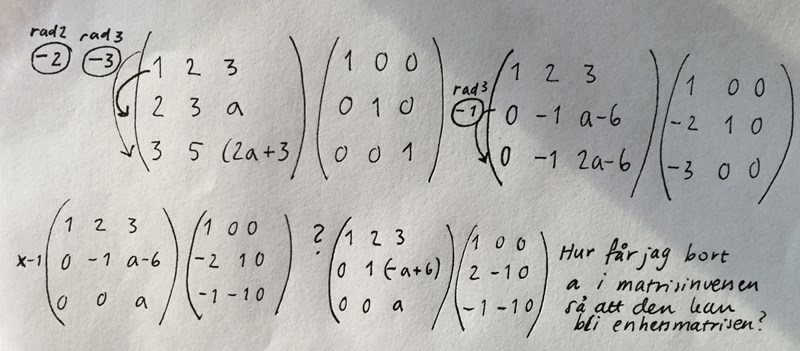
Hur jag får bort a i matrisen? Jag kan ju dela med a. 

$\frac{a}{a}=1$.

Jag fick slutligen fram en inversmatris som blev 

$\left(\begin{array}{ccc}-12& -7& 0\\ 8& 5& 0\\ -1& -1& 0\end{array}\right)$.

Jag multiplicerade den med kolonnvektorn $\left(\begin{array}{c}\begin{array}{c}2\\ 4\end{array}\\ b+6\end{array}\right)$ och fick då lösningen $\left(\begin{array}{c}\begin{array}{c}-52\\ 36\end{array}\\ -6\end{array}\right) dvs. x=-52, y=36 och z=-6.$

Då har jag fått den unika lösningen för när det(A)≠ 0, dvs när a ≠ 0.

Nu behöver jag också fylla i svaren för när det(A)=0 vilket sker när a=0.

När det(A)=0 saknas lösningar eller det finns oändligt antal lösningar. Om man sätter z=t, som man gjort i denna uppgift, så betyder det att man kan finna en parameterlösning där z kan vara vilket reellt tal som helst och man kan finna bestämda värden för x och y.

Hur kan jag nu bestämma värdena på x och y?

Och hur fungerar det med b som finns i HL?

När b=-6, då får vi ju en nolla i HL och det antar jag kan vara avgörande.

Vi har då en systemmatris och en lösningsvektor av detta utseende och ska svara på frågorna om värdena på b, x och y när a=0.

$\left(\begin{array}{ccc}1& 2& 3t\\ 2& 3& 0t\\ 3& 5& 3t\end{array}\right) \left(\begin{array}{c}2\\ 4\\ b+6\end{array}\right).$

Vad är b skilt från när a=0 och systemet saknar lösningar?

Vad har b, x och y för värden när z=”ett reellt tal kallat t” och a=0?

Behöver jag kanske göra om systemmatrisen till en matris på trappstegsform?

Jag tar tacksamt emot både kritik och goda råd :-)

EDIT: Ville bara tillägga att den korrekta inversmatrisen naturligtvis innehåller a. Det betyder att lösningen ovan inte är korrekt, men sättet som jag räknar ut lösningen är den som jag vill använda i uppgiften. 

Lisa Mårtensson skrev:

EDIT: Ville bara tillägga att den korrekta inversmatrisen naturligtvis innehåller a. Det betyder att lösningen ovan inte är korrekt, men sättet som jag räknar ut lösningen är den som jag vill använda i uppgiften. 

Jag skulle undvika att räkna ut inversen i detta problem då det är onödigt och ganska omständligt. Gör bara som Albiki skrev enligt nedan:

$\left[\begin{array}{ccc}1& 2& 3\\ 2& 3& a\\ 3& 5& 2a+3\end{array}\right]\left[\begin{array}{c}2\\ 4\\ b+6\end{array}\right] ~ \left[\begin{array}{ccc}1& 2& 3\\ 0& -1& a-6\\ 0& -1& 2a-6\end{array}\right]\left[\begin{array}{c}2\\ 0\\ b\end{array}\right]$ osv.

Alltså utför elementära radoperationer för att försöka få på trappstegsform. Du har tips i frågeställningen om vad dina slutliga alternativ att analysera kommer vara vilka är:

$$\begin{gathered} 1. a\ne 0 \\ 2. a=0 och b\ne 0 \\ 3. a=0 och b=0 \end{gathered}$$

z = t betyder att du anger en variabel som en parameter vilka övriga variabler kommer bero på. Det är bara ett sätt att beskriva lösningarna på när ett ekvationssystem har fler variabler än ekvationer. Alltså om till exempel rad 3 bara har nollor i sig.

Detta kommer till slut ge:

Lycka till!

Tack så mycket!

Det visade sig dessvärre att lösningarna som presenterades i spoilern inte stämde med facit. Det är en webbaserad uppgift så man kan bara se när man fyllt i rätt lösningar, inte vilka svar som önskas.

Jag har provat att framställa lösningarna på lite olika sätt, men utan framgång.

Tänkte att jag skulle kontrollräkna och se om jag kan hitta någon detalj som ska ändras.

Sen skulle jag behöva få förklarat för mig hur man kommerfram till detta:

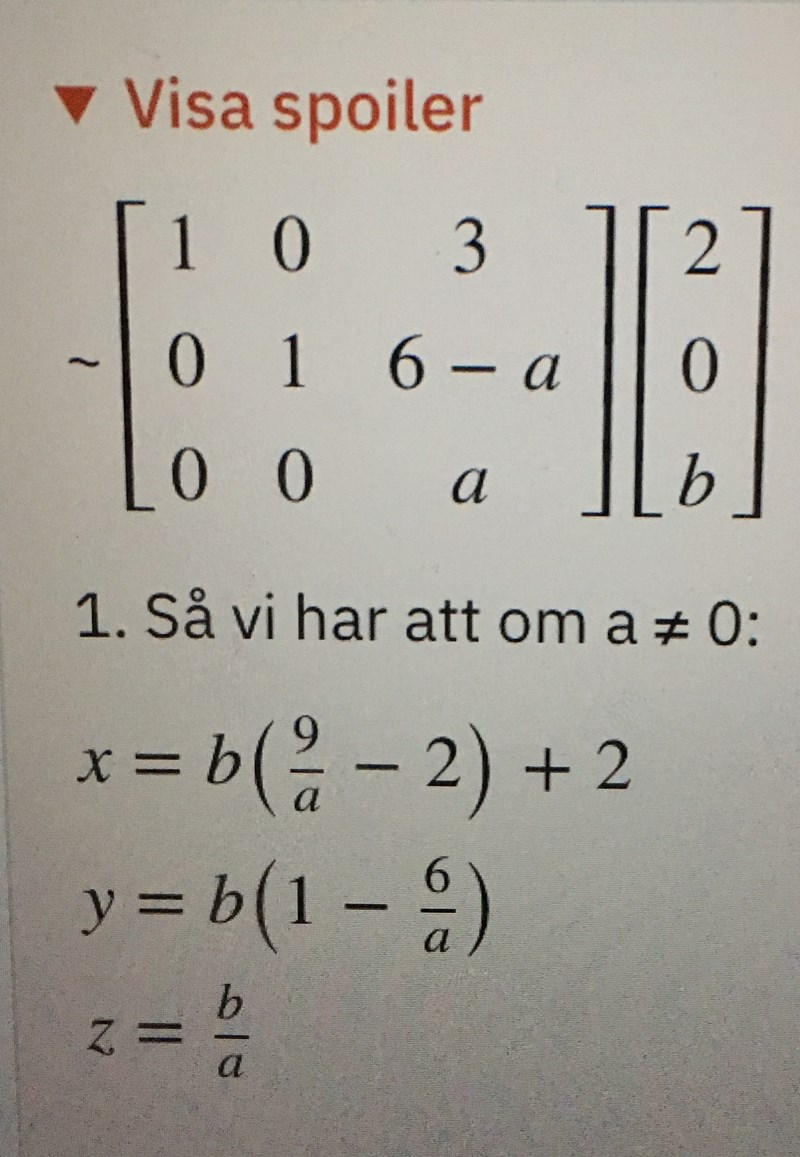
Hej!

Om $a\neq 0$ och $b=0$ är systemets totalmatris radekvivalent med matrisen 

    $\begin{pmatrix}1&0&0&2\\0&1&0&0\\0&0&1&0\end{pmatrix}.$

Om $a=0$ och $b\neq 0$ är systemets totalmatris radekvivalent med matrisen 

    $\begin{pmatrix}1&0&-9&0\\0&1&6&0\\0&0&0&1\end{pmatrix}$.

Om $a=0$ och $b=0$ är systemets totalmatris radekvivalent med matrisen 

    $\begin{pmatrix}1&0&-9&2\\0&1&6&0\\0&0&0&0\end{pmatrix}.$

Hej!

Björn Runows video "parameterlösning till linjärt ekvationssystem" ger jättebra förståelse. (Finns i spellistan Linjär algebra)

Edit: Youtube såklart :)

Tack! Jag ska titta på klippet och kommer att jobba med uppgiften i helgen! Har haft fullt upp på jobbet nu  i dagarna.

Lisa Mårtensson skrev:

Det visade sig dessvärre att lösningarna som presenterades i spoilern inte stämde med facit. Det är en webbaserad uppgift så man kan bara se när man fyllt i rätt lösningar, inte vilka svar som önskas.

Jag har provat att framställa lösningarna på lite olika sätt, men utan framgång.

Tänkte att jag skulle kontrollräkna och se om jag kan hitta någon detalj som ska ändras.

Sen skulle jag behöva få förklarat för mig hur man kommerfram till detta:

Du får ursäkta men jag trodde jag hade kollat igenom detta flera gånger om, tydligen inte. Jag gjorde någon knasig operation precis på slutet. Oberoende av detta borde du nog ha löst uppgiften med ledningen. För framtida referens, se nedan.

Koefficientmatrisen ovan från mitt resultat är fel så att få fram den genom radoperationer är omöjligt. Här är den ordentliga lösningen:

$\left[\begin{array}{ccc}1& 2& 3\\ 2& 3& a\\ 3& 5& 2a+3\end{array}\right]\left[\begin{array}{c}2\\ 4\\ b+6\end{array}\right] ~ \left[\begin{array}{ccc}1& 2& 3\\ 0& -1& a-6\\ 0& -1& 2a-6\end{array}\right]\left[\begin{array}{c}2\\ 0\\ b\end{array}\right] ~ \left[\begin{array}{ccc}1& 2& 3\\ 0& 1& 6-a\\ 0& 0& a\end{array}\right]\left[\begin{array}{c}2\\ 0\\ b\end{array}\right]$

Om du nu betraktar den sista matrisen som är på trappstegsform kan vi skriva om den till ett ekvationssystem för att vara övertydlig:

$\left\{\begin{array}{cccc}x+& 2y+& 3z& =2\\ & y+& (6-a)z& =0\\ & & az& =b\end{array}\right.$

1. Om $a\ne 0$ kan vi dividera med detta på tredje raden och bestämma $z=\frac{b}{a}$ vilket bestämmer övriga sekventiellt.

$$\begin{gathered} y+(6-a)\frac{b}{a}=0 \\ \iff \\ y=b(1-\frac{6}{a}) \end{gathered}$$

$$\begin{gathered} x+2b(1-\frac{6}{a})+3\frac{b}{a}=2 \\ \iff \\ x=2+b(\frac{9}{a}-2) \end{gathered}$$

2. Då $a=0$ men $b\ne 0$ ger precis som tidigare en situation där det i tredje raden står $0=b$ vilket är omöjligt så systemet har inga lösningar då.

3. Då $a=0$ och $b=0$ ser vi i utökade matrislösningen att vi får följande ekvationssystem:

$\left\{\begin{array}{cccc}x+& 2y+& 3z& =2\\ & y+& 6z& =0\end{array}\right.$ 

Detta ger att vi har fler okända än vi har ekvationer så vi får oändligt många lösningar i form av att två variabler kommer vara beroende av en tredje. Vi väljer $z=t$ vilket ger:

$\left\{\begin{array}{cc}x=& 2+9t\\ y=& -6t\\ z=& t\end{array}\right.$

Tack så oerhört mycket Ebola. Vilket arbete du lagt ner! Ditt svar är helt korrekt och stämmer med facit.

Jag håller precis med om att det är förståelsen för uppgiften som är viktig, inte att jag bara får veta rätt svar. 

Nu har jag bra förklaringar på denna länken inför liknande uppgifter.