Ekvationssystem med en lösning samt saknar lösning
Hej jag förstår inte riktigt hur man ska göra när det blir 3 okända. (2129)
Jag förstår att det gällande b) ”saknar lösning” innebär att de ska vara parallella.
men vad betyder det med endast en lösning? Vinkelräta?

Ekvationssystemets lösningar återfinns där motsvarande linjer möts.
Det innebär att ekvationssystemet
- saknar lösning då motsvarande linjer saknar skärningspunkt, dvs då de är parallella men åtskilda. Precis som du skrev.
- har exakt en lösning då linjerna möts på ett enda ställe, dvs då de skär varandra i en enda punkt. (De behöver inte vara vinkelräta.)
- har oändligt många lösningar då linjerna är identiska.
Okej! Men hur gör man när det finns flera obekanta?
Du kan skriva om de båda ekvstionerna på formen y = kx + m.
Då är det lättare att se vilka villkor som måste vara uppfyllda för att du ska få de tre olika fallen.
Jag har gjort såhär, men vet inte riktigt hur jag ska komma vidare
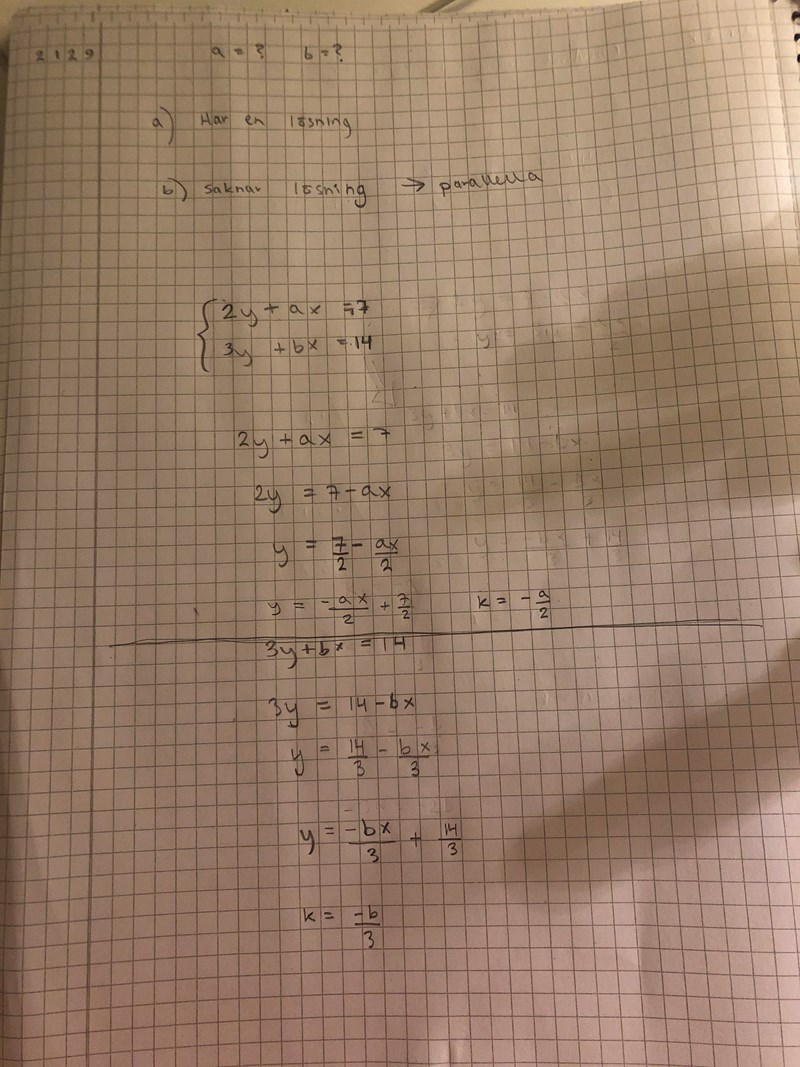
Bra början. Du har hittat k-värdena för de båda linjerna.
- Om två linjer har samma k-värde men olika m-värde så är det två olika parallella linjer, dvs två linjer som aldrig möts.
- Om två linjer har olika k-värde så möts de alltid i exakt en punkt, oavsett vilka m-värden de har.
Kommer du vidare då?
Jag förstår att man ska ta k1=K2, men vet inte hur man ska räkna ut det när det blir olika variabler inblandade där det inte går att bryta ut så att det bara blir en.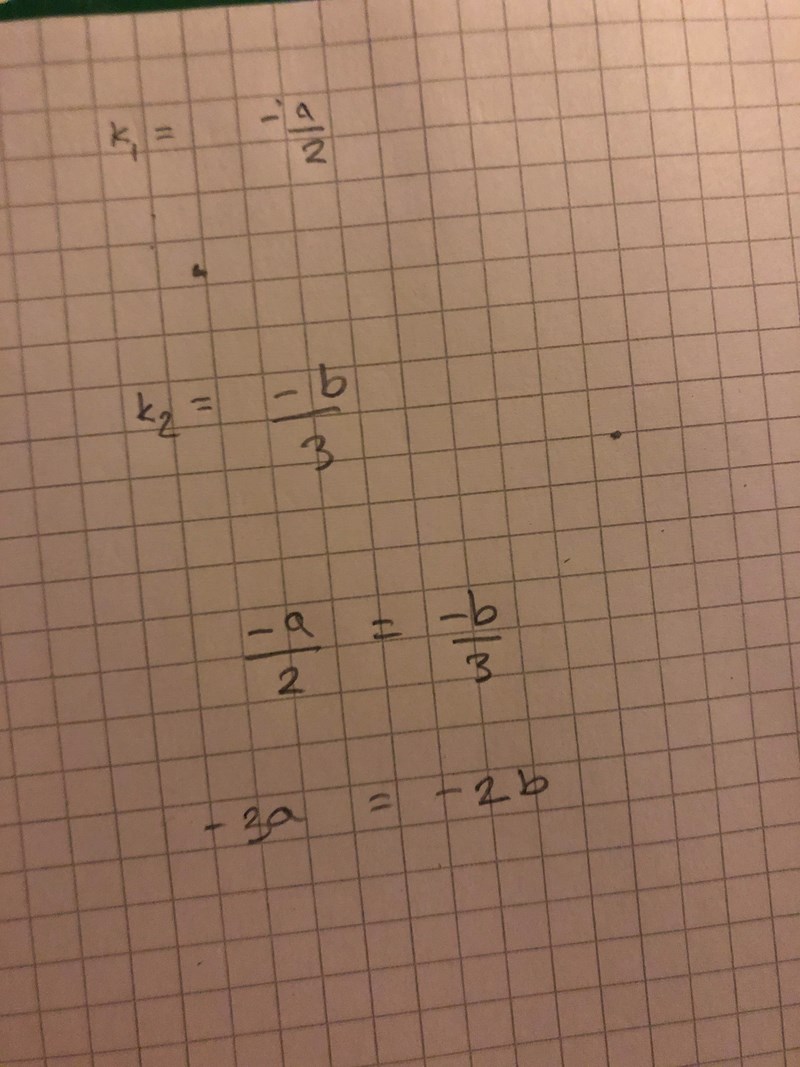
Ja det är rätt.
Du har hittat ett samband mellan a och b som, om det är uppfyllt, gör att ekvationssystemrt saknar lösning.
Sambabdet kan skrivas oå olika sätt, t.ex.
- 3a = 2b
- 3a - 2b = 0
- b = 1,5a
Okej tack! Och hur gör man när det bara ska vara en lösning? Kan man ställa upp det som ett vanligt ekvationssystem, eller hur gör man när det blir 4 obekanta totalt?
I det här fallet finns det oändligt många lösningar. För varje val av a finns ett bestämt värde på b enligt det samband du har hittat.
Rätt svar på frågan blir alltså
"Ekvationssystemet saknar lösning för alla värden på a och b som uppfyller sambandet b = 1,5a."
Du kan även välja något av de andra villkoren, men det är snyggast att ge ett svar där den ena obekanta variabeln står själv. Ett annat sätt att uttrycka samma sak är såklart .
De frågar inte efter ekvationssystemets lösning, så du behöver inte lösa ut vare sig x eller y. Därför har du bara två obekanta.
Kan du på samma sätt besvara frågan om vad som måste gälla för att ekvationssystemet ska ha exakt en lösning?
Jag vet tyvärr inte hur man ska göra för att få fram så att det bara finns en lösning
Läs det här svaret igen.
Alla värden som inte är a= 2b/3 ? Eftersom det saknades lösningar när det var k-värdet och att olika k-värden —-> möts i en punkt?
Just det.
Ja det stämmer.
Tack för hjälpen!




