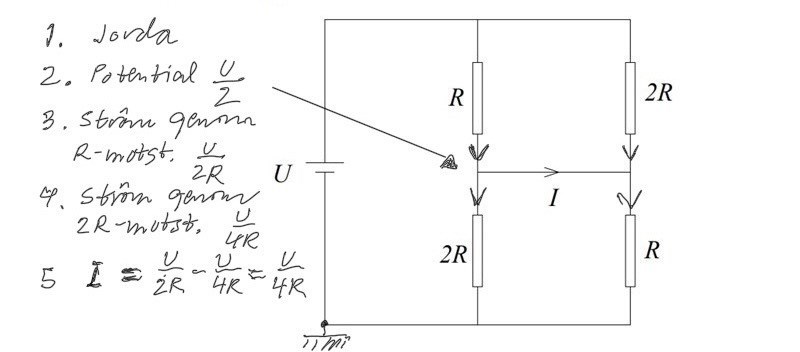
elektrisk krets
Hur löser man denna uppgift?
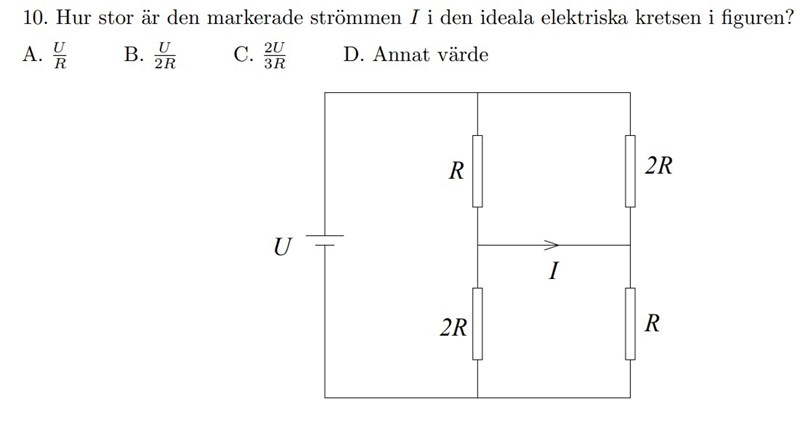
Du kan räkna ut svaret.
Eller man använder uteslutningsmetoden.
hur gör man för att räkna ut svaret?
RyanJ skrev:hur gör man för att räkna ut svaret?
Man börjar med att räkna ut ersättningsresistans och tragglar vidare.
Eller man ser att det är en halv U över alla dessa motstånd.
hur räknar man ut ersättningsresistansen? Har försökt göra det men förstår inte hur det fungerar när det blir en linje emellan.
RyanJ skrev:hur räknar man ut ersättningsresistansen? Har försökt göra det men förstår inte hur det fungerar när det blir en linje emellan.
Linjen är som en punkt, en nod. En kortslutning.
Du kan rita om det hela lite (på papper om du inte ser det för ditt inre öga).
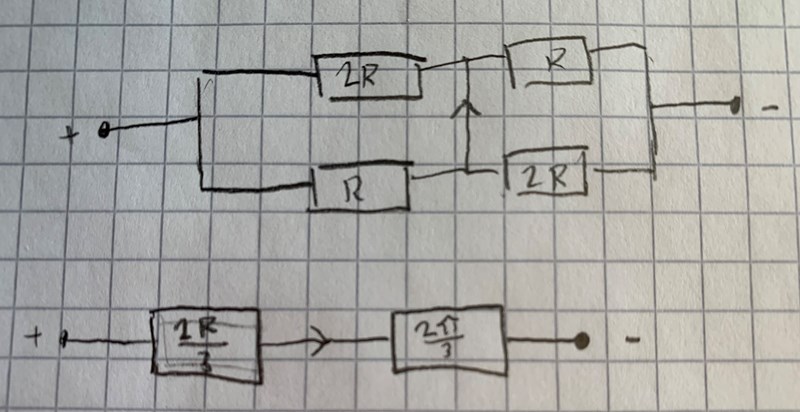 Så här?
Så här?
RyanJ skrev:Så här?
Nej.
Rita en nod mellan dessa fyra motstånd, som du ansluter alla dessa fyra mot.
Som om du hade riktiga sladdar och motstånd.
Såhär, men gärna snyggare:
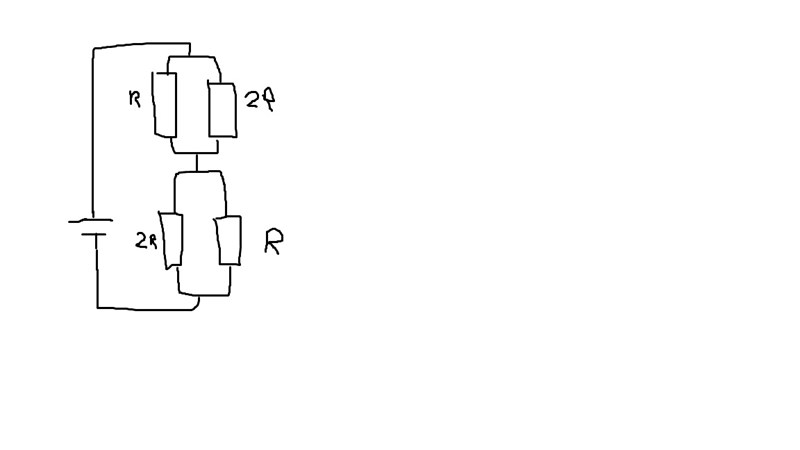
Ja, men bilden i inlägg #7 stämmer ju.
Laguna skrev:Ja, men bilden i inlägg #7 stämmer ju.
Hur menar du då? Båda seriemotstånd ska vara lika stora.
Smaragdalena skrev:Såhär, men gärna snyggare:
Hur kan det bli sådär?
Pieter Kuiper skrev:Laguna skrev:Ja, men bilden i inlägg #7 stämmer ju.
Hur menar du då? Båda seriemotstånd ska vara lika stora.
Står det inte 2R/3 på båda? Jag kanske bara vill att det ska göra det.
Laguna skrev:Pieter Kuiper skrev:Laguna skrev:Ja, men bilden i inlägg #7 stämmer ju.
Hur menar du då? Båda seriemotstånd ska vara lika stora.
Står det inte 2R/3 på båda? Jag kanske bara vill att det ska göra det.
aa, jag skrev 2R/3 på båda
Laguna skrev:Pieter Kuiper skrev:Laguna skrev:Ja, men bilden i inlägg #7 stämmer ju.
Hur menar du då? Båda seriemotstånd ska vara lika stora.
Står det inte 2R/3 på båda? Jag kanske bara vill att det ska göra det.
På den första läste jag "1R/3". Och den andra var kanske "2π/3"?
jaha, råka skriva pi istället för R på den andra. Men den första ska vara 2R/3
Det är inte lätt för oss att förstå vad du menar när du skriver något annat! Jag kan inte på stå att jag själv är oskyldig til detta misstag ibland.
RyanJ skrev:
Så här?
Och det är inte heller så tydligt med pilarna, men om du skulle mena att det är samma ström i båda kretsar så stämmer det inte.
ok. så hur löser man uppgiften?
RyanJ skrev:ok. så hur löser man uppgiften?
Du kan förstås bestämma strömmen genom varje motstånd.
och sen?
RyanJ skrev:och sen?
Kirchhoffs strömlag.
Jan Ragnar skrev:6
Jaha, fattar nu. Tack!
Och den snabba lösningen: man kan se direkt att det är halva spänningen över R, så strömmen genom det motståndet är (U/2)/R = U/2R. Den sökta strömmen I måste vara mindre så vi kan stryka A och B och C.
Anledningen för att det är halva spänningen över R, är väll för att om strömmen går genom det första R motståndet och sedan det andra R motståndet så måste spänningen för dessa vara samma, då resistansen är samma. Eller har jag fel?
RyanJ skrev:Anledningen för att det är halva spänningen över R, är väll för att om strömmen går genom det första R motståndet och sedan det andra R motståndet så måste spänningen för dessa vara samma, då resistansen är samma. Eller har jag fel?
Nja, det var inte tydligt. Och ofullständigt: de andra motståndens värden påverkar också.
Man kan se att det blir halva spänningen på grund av symmetri skulle jag säga.