Elektrisk och magnetisk fält
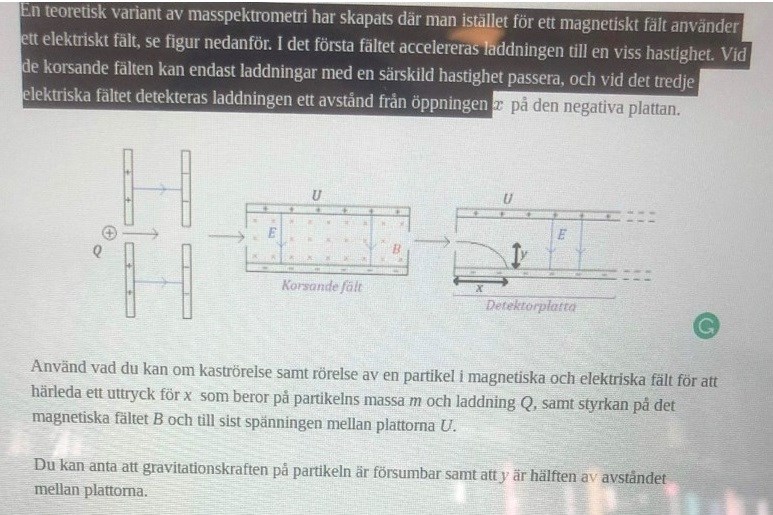
Jag vet inte hur jag ska lösa det och började med att dela uppgiften i tre delar.
först går protonen genom ett fält som får den att accelerera och då använde jag formeln UQ=W. Det nya Kinetiska energin (Wk) måste då vara ( mv0 ^ 2 ) / 2 + UQ = Wk. Alltså alla proton som kommer ut från detta fältet ha kinetiska energin ( mv0 ^ 2 ) / 2 + UQ.
Sedan går det igen till andra fältet och proton som kommer ut från det fältet måste ha hastigheten E/B. Då blir formeln ( mv0 ^ 2 ) / 2 + UQ = ( mE^2 )/ B^2
I tredje fältet försökte jag använda formlerna x= v0tCos(a) och y= v0tsin(a) - (at^2) / 2 men vet inte hur kan kombinera det med ( mv0 ^ 2 ) / 2 + UQ = ( mE^2 )/ B^2
I det korsande fältet väljs de partiklar som har hastigheten med riktning rakt åt höger ut. Av uppgiftstexten får vi också veta att
Nu kan du använda samma strategi som i du använde i uppgiften https://www.pluggakuten.se/trad/elektrisk-falt-38/
Beräkna först tiden partikeln befinner sig i fältet. Uttrycket kommer innehålla .
Ställ sedan upp ekvationen i y-led.
D4NIEL skrev:I det korsande fältet väljs de partiklar som har hastigheten med riktning rakt åt höger ut. Av uppgiftstexten får vi också veta att
Nu kan du använda samma strategi som i du använde i uppgiften https://www.pluggakuten.se/trad/elektrisk-falt-38/
Beräkna först tiden partikeln befinner sig i fältet. Uttrycket kommer innehålla .
Ställ sedan upp ekvationen i y-led.
Men stämmer mina räkningar på första och andra fältet?
Du har korrekt kommit fram till att hastigheten när partikeln lämnar det andra fältet är
Men du har också antagit att spänningen mellan de vertikala plattorna i det första fältet är U, vilket inte framgår ur figuren. Dessutom spelar det ingen roll eftersom det korsande fältet fungerar som ett filter som bara släpper igenom partiklar av en visst hastighet.
Vill du göra en energibetraktelse är det lättast att sätta potentialen för "höjden" i det tredje fältet till . Efter det andra fältet kan du notera att rörelseenergin är vid inträdet i det tredje fältet. Alltså har partikeln den totala energin
Vid inträdet i det tredje fältet. När den når plattan efter har den energin
Energin bevaras eftersom det elektriska fältet är konservativt.
D4NIEL skrev:sätta potentialen för "höjden" i det tredje fältet till . Efter det andra fältet kan du notera att rörelseenergin är vid inträdet i det tredje fältet. Alltså har partikeln den totala energin
Vad menar du med att sätta höjden y till U/2 menar du E=U/2y?
Ja, ungefär.
När du räknar med den vanliga lägesenergin måste du införa en godtycklig nollnivå. Ofta vid markytan.
På samma sätt måste man införa en godtycklig nollnivå när man räknar med en elektrisk potential.
Om vi sätter nollnivån vid den undre plattan är potentialen vid höjden y helt enkelt det elektriska fältet (V/m) gånger sträckan y(m), dvs
Eftersom fältet är blir potentialen helt enkelt
Är du med?

