Elementa årgång 57 problem nummer 2965
(Alla problem från den nedlagda tidskriften Elementa finns här:
http://www.swe-math-soc.se/Elementaproblemen/
)
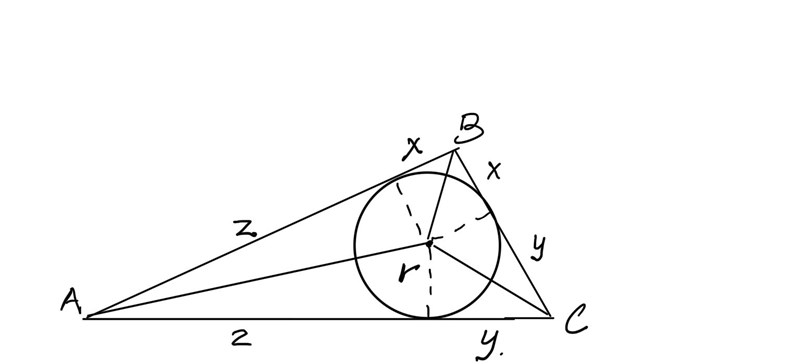
För att komma igång med Elementa-uppgiften lägger jag in en inskriven cirkel i triangeln.
Triangelns omkrets är 2x + 2y + 2z.
Halva omkretsen p = x + y + z
Låter som en bra metod. Då får du ju halva vinklarna på köpet!
Vi fortsätter med halva omkretsen
p = r*cot(B/2) + r*cot(C/2) + r*cot(A/2) = r*[cot(A/2) + cot(B/2) + cot(C/2)] =
= r*[cot(A/2)*cot(B/2)*cot(C/2)]
Om vinklarna α + β + γ = 90˚ så gäller det att
cot(α) + cot(β) + cot(γ) = cot(α)*cot(β)*cot(γ)
Ytan T = 2*(r*x/2) + 2*(r*y/2) + 2*(r*z/2) = r*(x + y + z) = r*p =
= p*tan(A/2)*tan(B/2)*tan(C/2)*p
”The triple cotangent identity” var inte något som ingick i matematiken vid min gymnasieutbildning i Göteborg på 60-talet. Troligen var det först som pensionär jag stötte på den i Eli Maors utmärkta bok Trigonometric Delights, utgiven 1998. Boken finns inte översatt till svenska, men vållar troligen inga stora problem för dagens gymnasister med bra engelskakunskaper. För de första tre fjärdedelarna av boken räcker det med gymnasiekunskaper. För den sista fjärdedelen behövs nog en termin på universitet eller motsvarande.
Wikipedia har förstås information om tangens- och cotangenssatser.
https://en.wikipedia.org/wiki/Proofs_of_trigonometric_identities#Tangent_and_cotangent
https://press.princeton.edu/books/paperback/9780691158204/trigonometric-delights
Vill tacka henrikus för att Du återupplivade minnet av Elementa, som jag prenumererade på under ett antal år under 60-talet.
Visa spoiler
Snyggt bevis! Snyggare än mitt som använde Herons formel.
Bevis av "the triple cotangent identity" i spoilern