Elementära funktioner (2)

Annat alternativ är att använda trigonometriska ettan.

Det är väl det jag har gjort?

Du hade inte gjort det innan du redigerade inlägget.

Jag avsåg att du kunde gjort det som ett första steg för att göra så att ditt problem endast har cosinus is sig och inte både cosinus och sinus. Att se till att uttrycket man jobbar med endast har en typ av trigonometrisk funktion är i regel ett användbart trick för att förenkla problemet.

Vill du fortsätta med.tråden du löpt hittills rekommenderar jag att du jämför med sinus för dubbla vinkeln.

Jag har räknat och försökt lösa uppgiften på smidigaste sätt. Finns det smidigare/enklare varianter att lösa på får man gärna hojta till! 

Menar du att jag ska använda mig utav ${\sin }^2\left(x\right)=\frac{1-\cos \left(2x\right)}{2}$?

Alternativ 1. Använd trigonometriska ettan för att göra problemet till ett cosinusproblem

$(\cos^2(x))^2 + (\sin^2(x))^2 = \frac{1}{2}$

$(\cos^2(x))^2 + (1 - \cos^2(x))^2 = \frac{1}{2}$

$2(\cos^2(x))^2 - 2 \cos^2(x)^2 + 1 = \frac{1}{2}$

Detta är effektivt en andragradsekvation.

Alternativ 2. Används tricket du gjorde i sin lösning och när du kommer till

$2 \cos^2 (x) \sin^2(x) = - \frac{1}{2}$

används sinus för dubbla vinkeln $\sin(2x) = 2 \sin(x) \cos(x)$ för att skriva om ekvaitonen som

$\frac{1}{2} (2\cos(x) \sin(x))^2 = - \frac{1}{2}$

$\frac{1}{2} \sin^2(2x) = - \frac{1}{2}$

Senaste uträkningen:

$$\begin{gathered} 1-2{\cos }^2\left(x\right){\sin }^2\left(x\right)=\frac{1}{2} \\ 2{\cos }^2\left(x\right){\sin }^2\left(x\right)-1=-\frac{1}{2} \\ 2{\cos }^2\left(x\right){\sin }^2\left(x\right)=\frac{1}{2} \\ \frac{1}{2}\left(2{\cos }^2\right(x\left){\sin }^2\right(x){)}^2=\frac{1}{2} \\ \frac{1}{2}({\sin }^2\left(2x\right))=\frac{1}{2} \\ {\sin }^2(2x)=1 \\ \sin (2x)=\pm 1 \\ 2x=arc\sin (\pm 1) \\ 2x_1=\frac{-\mathrm{\pi }}{2}+k2\mathrm{\pi }, 2{\mathrm{x}}_2=\frac{\mathrm{\pi }}{2}+\mathrm{k}2\mathrm{\pi } \\ {\mathrm{x}}_1=\frac{-\mathrm{\pi }}{4}+\mathrm{k\pi }, {\mathrm{x}}_2=\frac{\mathrm{\pi }}{4}+\mathrm{k\pi } \end{gathered}$$

I facit står endast $x_2$. Varför gör det det? $\cos \left(v\right)=\cos (-v)$ samt $\sin \left(v\right)=-\sin \left(v\right)\to {\sin }^4(-v)={\sin }^4\left(v\right)$

Eller är jag fredagstrött?

Föraren skrev :

Senaste uträkningen:

$$\begin{gathered} 1-2{\cos }^2\left(x\right){\sin }^2\left(x\right)=\frac{1}{2} \\ 2{\cos }^2\left(x\right){\sin }^2\left(x\right)-1=-\frac{1}{2} \\ 2{\cos }^2\left(x\right){\sin }^2\left(x\right)=\frac{1}{2} \\ \frac{1}{2}\left(2{\cos }^2\right(x\left){\sin }^2\right(x){)}^2=\frac{1}{2} \\ \frac{1}{2}({\sin }^2\left(2x\right))=\frac{1}{2} \\ {\sin }^2(2x)=1 \\ \sin (2x)=\pm 1 \\ 2x=arc\sin (\pm 1) \\ 2x_1=\frac{-\mathrm{\pi }}{2}+k2\mathrm{\pi }, 2{\mathrm{x}}_2=\frac{\mathrm{\pi }}{2}+\mathrm{k}2\mathrm{\pi } \\ {\mathrm{x}}_1=\frac{-\mathrm{\pi }}{4}+\mathrm{k\pi }, {\mathrm{x}}_2=\frac{\mathrm{\pi }}{4}+\mathrm{k\pi } \end{gathered}$$

I facit står endast $x_2$. Varför gör det det? $\cos \left(v\right)=\cos (-v)$ samt $\sin \left(v\right)=-\sin \left(v\right)\to {\sin }^4(-v)={\sin }^4\left(v\right)$

Eller är jag fredagstrött?

Det står nog inte exakt som ditt $x_2$ i facit.

Visst står det $x=\frac{\mathrm{\pi }}{4}+k\frac{\mathrm{\pi }}{2}$ (eller motsvarande), dvs med periodicitet $\frac{\mathrm{\pi }}{2}$?

---------------------------------------

Du kan nämligen slå ihop lösningsmängderna för $2x_1$ och $2x_2$ till följande: $2x=\frac{\mathrm{\pi }}{2}+k\mathrm{\pi }$

Då får du att $x=\frac{\mathrm{\pi }}{4}+k\frac{\mathrm{\pi }}{2}$

Du tänkte nog rätt, men råkade skriva fel och fick med extra exponenter på en rad (rödmarkerade).

Men de försvann sedan igen.

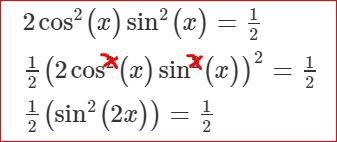
Tack för att ni har extra koll, fel av mig. I facit står $x=\frac{\mathrm{\pi }}{4}+k\frac{\mathrm{\pi }}{2}$. Förlåt.

Föraren skrev :

Tack för att ni har extra koll, fel av mig. I facit står $x=\frac{\mathrm{\pi }}{4}+k\frac{\mathrm{\pi }}{2}$. Förlåt.

Det finns ingen anledning att be om förlåtelse. Det här är ju vad Pluggakuten handlar om!

Jag förstår dock inte hur du slår ihop $2x_1$ och $2x_2$. Går det att förklara lite mer i detalj?

Föraren skrev :

Jag förstår dock inte hur du slår ihop $2x_1$ och $2x_2$. Går det att förklara lite mer i detalj?

Alternativ 1: Inspektera de två lösningsmängderna och skriv upp de första lösningarna i var och en:

$\mathbf{2}{\mathit{x}}_{\mathbf{1}}\mathbf{:}\mathbf{ }\mathbf{-}\frac{\mathbf{\pi }}{\mathbf{2}}\mathbf{,}\mathbf{ }\frac{\mathbf{3}\mathbf{\pi }}{\mathbf{2}}\mathbf{,}\frac{\mathbf{7}\mathbf{\pi }}{\mathbf{2}}\mathbf{,}\frac{\mathbf{11}\mathbf{\pi }}{\mathbf{2}}\mathbf{,}\frac{\mathbf{15}\mathbf{\pi }}{\mathbf{2}}$ och så vidare.

$\mathbf{2}{\mathit{x}}_{\mathbf{2}}\mathbf{:}\mathbf{ }\frac{\mathbf{\pi }}{\mathbf{2}}\mathbf{,}\mathbf{ }\frac{\mathbf{5}\mathbf{\pi }}{\mathbf{2}}\mathbf{,}\frac{\mathbf{9}\mathbf{\pi }}{\mathbf{2}}\mathbf{,}\frac{\mathbf{13}\mathbf{\pi }}{\mathbf{2}}\mathbf{,}\frac{\mathbf{17}\mathbf{\pi }}{\mathbf{2}}$ och så vidare.

Om vi skriver ihop dessa i en ordnad följd får vi:

$\mathbf{-}\frac{\mathbf{\pi }}{\mathbf{2}},\mathbf{ }\frac{\mathbf{\pi }}{\mathbf{2}},\mathbf{ }\frac{\mathbf{3}\mathbf{\pi }}{\mathbf{2}},\frac{\mathbf{5}\mathbf{\pi }}{\mathbf{2}},\frac{\mathbf{7}\mathbf{\pi }}{\mathbf{2}},\frac{\mathbf{9}\mathbf{\pi }}{\mathbf{2}},\frac{\mathbf{11}\mathbf{\pi }}{\mathbf{4}},\frac{\mathbf{13}\mathbf{\pi }}{\mathbf{2}},\frac{\mathbf{15}\mathbf{\pi }}{\mathbf{2}},\frac{\mathbf{17}\mathbf{\pi }}{\mathbf{2}}$ och så vidare.

Denna följd kan på ett enklare sätt skrivas som $\frac{\mathrm{\pi }}{2}+k\mathrm{\pi }$ 

Alternativ 2: Dela inte ens upp det i två lösningsmängder från början. Du har att $\sin \left(2x\right)=\pm 1$. Efter att ha tillfrågat oraklet Enhetscirkeln Den Allvetande så inser vi direkt att denna ekvation (egentligen dessa ekvationer) har lösningsmängden $2x=\frac{\mathrm{\pi }}{2}+k\mathrm{\pi }$.

Super!