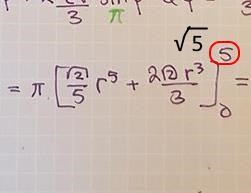Eliptiska koordinater

Den här uppgiften kommer ge dig lite krångliga integraler, men av olika sort beroende på hur du väljer att räkna.

Om ni har gått igenom sfäriska koordinater tror jag att det ger dig bekvämast integraler.

$x=\frac{1}{\sqrt{2}}r\sin(\theta)\cos(\varphi)$

$y=-1+r\sin(\theta)\sin(\varphi)$

$z=-2+r\cos(\theta)$

Kroppen $2x^2+y^2+z^2+2y+4z\leq 0$ blir då det vackra $r^2\leq 5$

Om du inte räds integraler av typen $\displaystyle \int r^n\sqrt{5-r^2}\,dr$ och/eller känner dig mer bekväm med planpolära koordinater kan du använda

$x=\frac{1}{\sqrt{2}}r\cos(v)$

$y=-1+r\sin(v)$

Kroppen reduceras då till (det lite krångligare) $(z+2)^2\leq 5-r^2$

I båda fallen kommer du ha nytta av följande:

$\displaystyle \int_0^{2\pi}\sin(u)\,\mathrm{d}u=\int_0^{2\pi}\cos(u)\,\mathrm{d}u=0$

$\displaystyle \int_0^{2\pi}\sin^2(u)\,\mathrm{d}u=\int_0^{2\pi}\cos^2(u)\,\mathrm{d}u=\pi$

Jroth skrev:

Den här uppgiften kommer ge dig lite krångliga integraler, men av olika sort beroende på hur du väljer att räkna.

Om ni har gått igenom sfäriska koordinater tror jag att det ger dig bekvämast integraler.

$x=\frac{1}{\sqrt{2}}r\sin(\theta)\cos(\varphi)$

$y=-1+r\sin(\theta)\sin(\varphi)$

$z=-2+r\cos(\theta)$

Kroppen $2x^2+y^2+z^2+2y+4z\leq 0$ blir då det vackra $r^2\leq 5$

Om du inte räds integraler av typen $\displaystyle \int r^n\sqrt{5-r^2}\,dr$ och/eller känner dig mer bekväm med planpolära koordinater kan du använda

$x=\frac{1}{\sqrt{2}}r\cos(v)$

$y=-1+r\sin(v)$

Kroppen reduceras då till (det lite krångligare) $(z+2)^2\leq 5-r^2$

I båda fallen kommer du ha nytta av följande:

$\displaystyle \int_0^{2\pi}\sin(u)\,\mathrm{d}u=\int_0^{2\pi}\cos(u)\,\mathrm{d}u=0$

$\displaystyle \int_0^{2\pi}\sin^2(u)\,\mathrm{d}u=\int_0^{2\pi}\cos^2(u)\,\mathrm{d}u=\pi$

Tack! Jag provar med sfäriska koordinater så får vi se var de tar mig 😀

Jag kanske också ska nämna att man kan lägga "bollen" i origo och sedan parallellförflytta tröghetsmomentet med hjälp av Steiners sats

https://sv.wikipedia.org/wiki/Parallellaxelteoremet

Jroth skrev:

Jag kanske också ska nämna att man kan lägga "bollen" i origo och sedan parallellförflytta tröghetsmomentet med hjälp av Steiners sats

https://sv.wikipedia.org/wiki/Parallellaxelteoremet

Asså jag provade med sfäriska koordinater, men måste gjort fel ngn stans 🙈

Louiger skrev:

Jroth skrev:

Jag kanske också ska nämna att man kan lägga "bollen" i origo och sedan parallellförflytta tröghetsmomentet med hjälp av Steiners sats

https://sv.wikipedia.org/wiki/Parallellaxelteoremet

Asså jag provade med sfäriska koordinater, men måste gjort fel ngn stans 🙈

Ser att jag satte r till 5 ska ju vara sqrt5 provar igen!

Ser riktigt bra ut. Rätt tänkt och rätt räknat! Ett litet slarvfel med integrationsgränsen bara...

Edit: Du verkade hitta felet själv under tiden jag paintade, bra jobbat :) Låter min post stå kvar för eftervärlden.

--------------------------------------------------------------------------------------------