Elkretsproblem, bestäm u(t) för t>0

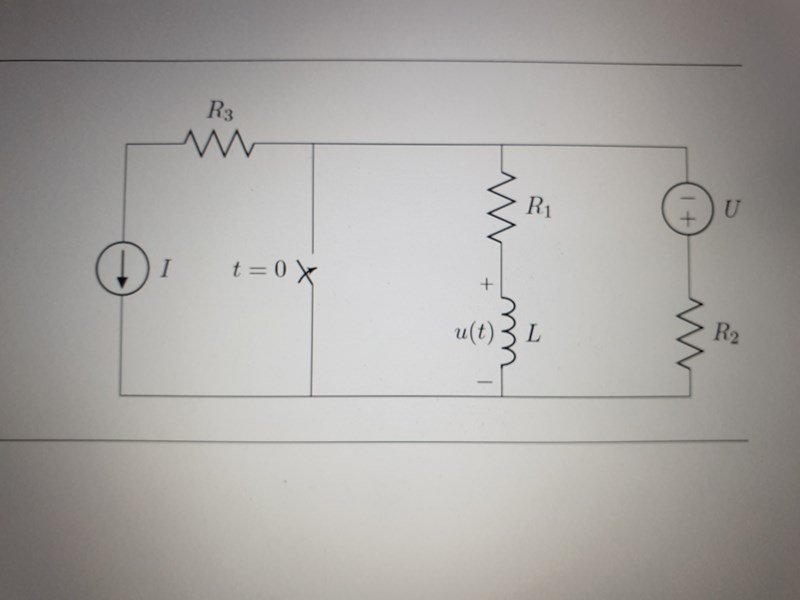
hitta u(t) för t>0

Det finns 3 olika tidsstadier att ta hänsyn till, innan t(0-), precis efter t(0+) och långt efter t(∞)

Den generella lösningen ges av u(t) = u(∞) + (u(0+)-u(∞))e(-t/τ), där τ = CR = L/R.

Vid t(0-) och t(∞), equilibrium, är C en öppen krets och L är en stängd krets

vid t(0+), continuity, beter sig C och L som en spänningskälla respektive strömkälla, här under är mina beräkningar än så länge.

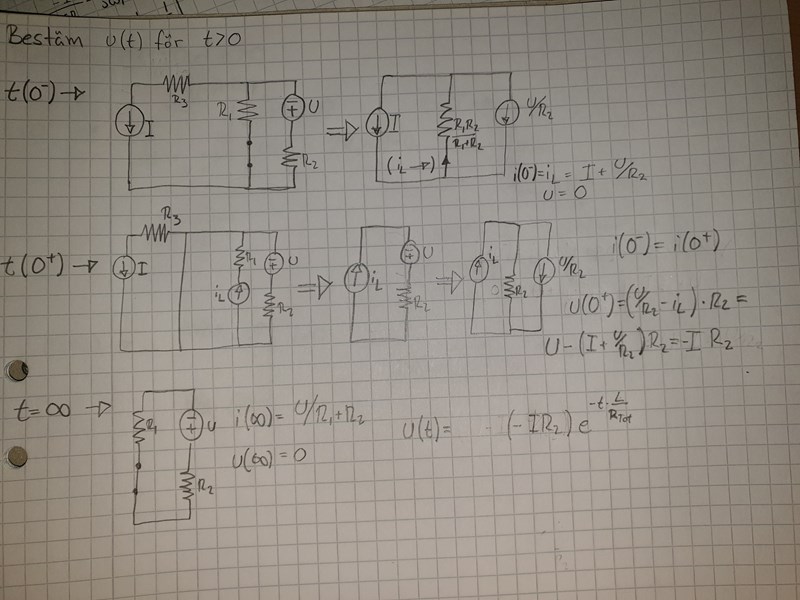
Vi börjar med det enklaste.

$u (t \to \infty) = 0$

Spolen har noll impedans för likström (ström som inte ändrar sig)

Således kan vi lika enkelt följa upp med

$u (t -) = 0$

Före det att strömbrytaren sluts, ändrar sig inte strömmen ( $u = L \frac{d i}{d t}$ ) i spolen

För t = t- skriver vi:

$I R_{3} = I_{L} R_{1} I_{L} = \frac{R_{3}}{R_{1_{}}} I$

Där I_L är strömmen i(t=0) genom spolen

För tiden t=t+ skriver vi

$L \frac{d i (t)}{d t} + i (t) R_{1} = 0 \frac{d i (t)}{d t} + \frac{R_{1}}{L} i (t) = 0$

...en rudimentär diff-ekvation...

Tack för hjälpen, jag behöver dock svaret i den generella formen "u(t) = u(∞) + (u(0+)-u(∞))e(-t/τ)" och har väldigt svårt att göra det utifrån d.e. formen som du har gjort, vad är u(0⁺) och i(t) till exempel?

the fifth of November skrev:
Tack för hjälpen, jag behöver dock svaret i den generella formen "u(t) = u(∞) + (u(0+)-u(∞))e(-t/τ)" och har väldigt svårt att göra det utifrån d.e. formen som du har gjort, vad är u(0⁺) och i(t) till exempel?

$i' (t) + \frac{R_{1}}{L} i (t) = 0 i (t) = A e^{- \frac{R_{1}}{L} t} i (t = 0) = A = \frac{R_{3}}{R_{1}} I u (t) = L i' (t) = . . . .$

the fifth of November skrev:
Tack för hjälpen, jag behöver dock svaret i den generella formen "u(t) = u(∞) + (u(0+)-u(∞))e(-t/τ)" och har väldigt svårt att göra det utifrån d.e. formen som du har gjort, vad är u(0⁺) och i(t) till exempel?

Den generella formen reduceras till:

$u (t) = u (t +) e^{- t / τ}$

Du tar fram strömmen $i (t)$ genom att lösa differentialekvationen. Vet du hur man gör?

nej jag vet inte hur man gör tyvärr

the fifth of November skrev:
nej jag vet inte hur man gör tyvärr

Men om du tittar på mitt senaste inlägg, så ser du hur man gör :-)

Ja nu såg jag det, mitt fel som missade det.

Så enligt mina (dina) beräkningar så är i'(t) = -(IR3/L)e^-(R₁/L)t och u(t) = Li'(t) = -(IR₃)e^-(^R₁/L)t, ser det bra ut?

Jo, det ser bra ut 🙂

Svara

Visa senaste svar