Ellära - Beräkna resistansen

Beräkna resistansen mellan punkterna A och B i nedanstående koppling.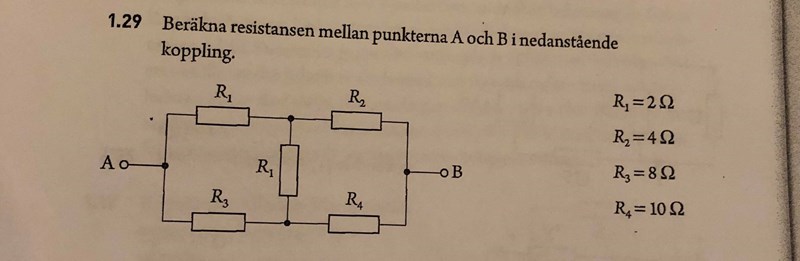

Har testat olika sätt, men har ingen aning om hur jag ska gå till väga här. Rätt svar är R = 4,47 Ω.

Jag tänker såhär:

R1&R2 är en seriekoppling. R3&R4 är en seriekoppling. R1&R1 är en seriekoppling. R3&R1 är en seriekoppling. R1&R3 är, om man bortser från den andra R1 i mitten, en parallellkoppling. Samma gäller för R2&R4. Men jag förstår inte hur eller var man ska applicera den R1 som är i mitten.

Väldigt tacksam för all hjälp!

Tänk så här: Kommer det gå någon strömm igenom $R_{1}$ (Den i mitten)?

Kom på mig själv. Det kommer gå en väldigt svag strömm geom R1

Men har du hört om kirchhoffs lagar?

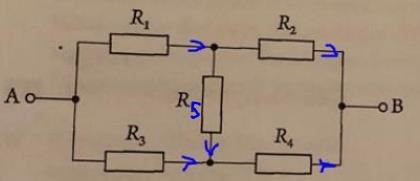
Jag börjar med att för enkelhets skull kalla den lodräta resistansen för R₅ och den sökta resistansen för R

Nämnaren i den första ekvationen representerar ett slags medelvärde av strömmarna i de båda horisontella ledningarna. Det försvinner ju ingen ström mellan A och B, bara för att man lagt till R₅

$R = \frac{U_{A B}}{(\frac{I_{1} + I_{2}}{2} + \frac{I_{3} + I_{4}}{2})} U_{A B} = R_{1} I_{1} + R_{2} I_{2} U_{A B} = R_{3} I_{3} + R_{4} I_{4} U_{A B} = R_{1} I_{1} + R_{5} I_{5} + R_{4} I_{4} U_{A B} = R_{3} I_{3} - R_{5} I_{5} + R_{2} I_{2} I_{2} = I_{1} - I_{5} I_{4} = I_{3} + I_{5}$

Jaha, det var sju obekanta och sju ekvationer :-)

Affe Jkpg skrev:
Jag börjar med att för enkelhets skull kalla den lodräta resistansen för R₅ och den sökta resistansen för R
Nämnaren i den första ekvationen representerar ett slags medelvärde av strömmarna i de båda horisontella ledningarna. Det försvinner ju ingen ström mellan A och B, bara för att man lagt till R₅
$R = \frac{U_{A B}}{(\frac{I_{1} + I_{2}}{2} + \frac{I_{3} + I_{4}}{2})} U_{A B} = R_{1} I_{1} + R_{2} I_{2} U_{A B} = R_{3} I_{3} + R_{4} I_{4} U_{A B} = R_{1} I_{1} + R_{5} I_{5} + R_{4} I_{4} U_{A B} = R_{3} I_{3} - R_{5} I_{5} + R_{2} I_{2} I_{2} = I_{1} - I_{5} I_{4} = I_{3} + I_{5}$
Jaha, det var sju obekanta och sju ekvationer :-)

Strömriktningarna jag använder i ekvationerna

Man kan börja med det enklaste....

$1 : R = \frac{2 U_{A B}}{I_{1} + I_{2} + I_{3} + I_{4}} 2 : U_{A B} = R_{1} I_{1} + R_{2} I_{2} 3 : U_{A B} = R_{3} I_{3} + R_{4} I_{4} 4 : U_{A B} = R_{1} I_{1} + R_{5} I_{5} + R_{4} I_{4} 5 : U_{A B} = R_{3} I_{3} - R_{5} I_{5} + R_{2} I_{2} 6 : I_{2} = I_{1} - I_{5} 7 : I_{4} = I_{3} + I_{5}$

Sedan tänker jag att man kan t.ex. söka ett läge som kan beskrivas som:

$R = \frac{I_{n} * f_{1} (R_{k})}{I_{n} * f_{2} (R_{k})} 1 \leq k \leq 5$

Då kan man förkorta med I_n och uppgiften är löst :-)

Använder man först genomgående "6:" och "7": och eliminerar "U_AB" återstår fyra ekvationer med fyra obekanta.

Då använder jag "6:" och "7:" i "1:" till "5:"

$1 a : R = \frac{2 U_{A B}}{2 I_{1} + 2 I_{3}} 2 a : U_{A B} = R_{1} I_{1} + R_{2} (I_{1} - I_{5}) 3 a : U_{A B} = R_{3} I_{3} + R_{4} (I_{3} + I_{5}) 4 a : U_{A B} = R_{1} I_{1} + R_{5} I_{5} + R_{4} (I_{3} + I_{5}) 5 a : U_{A B} = R_{3} I_{3} - R_{5} I_{5} + R_{2} (I_{1} - I_{5})$

Så renskriver jag ovanstående

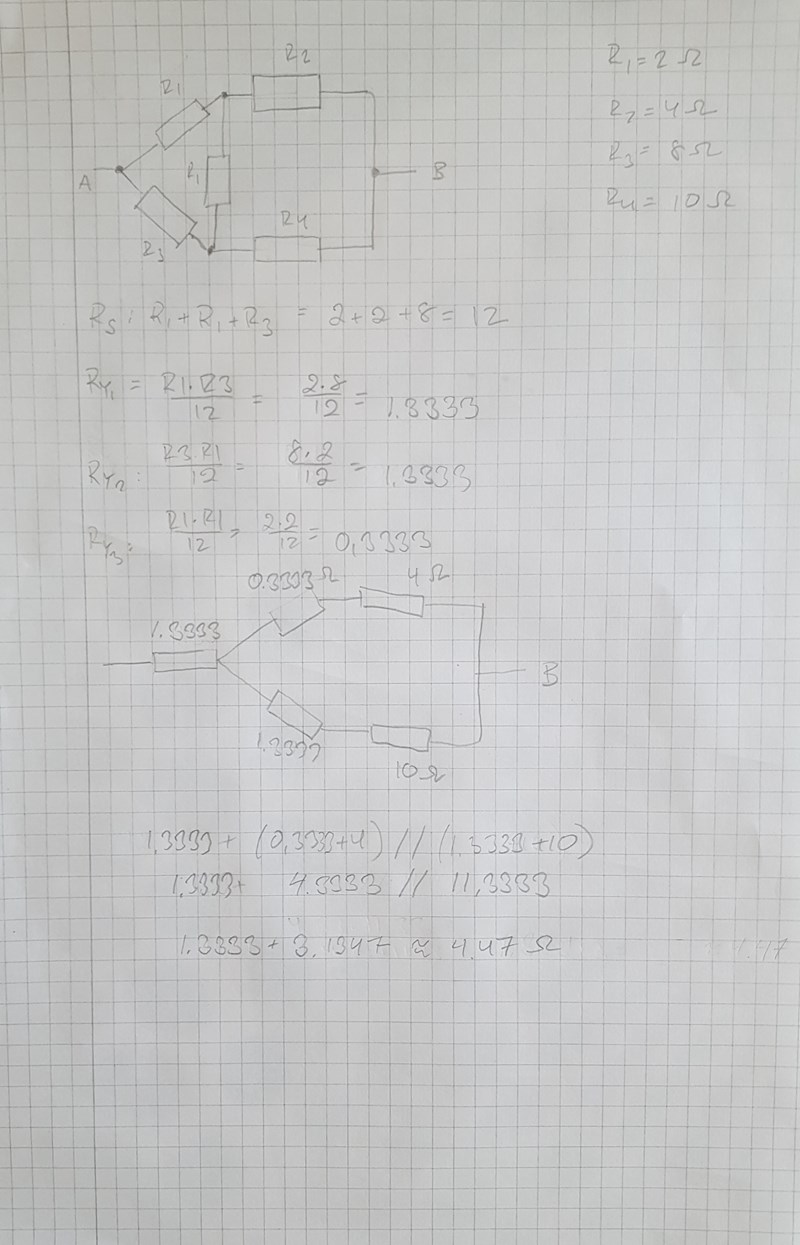
$1 a : R = \frac{U_{A B}}{I_{1} + I_{3}} 2 a : U_{A B} = (R_{1} + R_{2}) I_{1} - R_{2} I_{5} 3 a : U_{A B} = (R_{3} + R_{4}) I_{3} + R_{4} I_{5} 4 a : U_{A B} = R_{1} I_{1} + R_{4} I_{3} + (R_{4} + R_{5}) I_{5} 5 a : U_{A B} = R_{2} I_{1} + R_{3} I_{3} - (R_{2} + R_{5}) I_{5}$

Har löst uppgiften på följande sätt och det verkar vara rätt i facit.

Min fråga är följande: kan man använda sättet som jag har gjort?

Svara

Visa senaste svar