Ems, effekt och resistans
Hej.
Jag behöver hjälp med följande uppgift:

Jag började med att uttrycka effekten enbart i Ry och tänkte sedan beräkna maximivärdet för funktionen. Men P(Ry) blir väldigt krånglig och det känns som att det finns ett smidigare sätt. Boken har aldrig tidigare gjort liknande uppgifter och jag undrar hur jag ska komma vidare/göra på annat sätt.

Klurigt det där!
Antingen vet man att det finns något som heter Maximum power transfer theorem vilket säger att lastens resistans skall vara samma som den inre resistansen för maximalt effektuttag.
Eller så ser man att det är två seriekopplade resistorer, tar fram U=R*I och P=U*I. Sedan får man ett ganska jobbigt uttryck där man behöver finna ett maximum för P. Då behöver man antagligen derivera och det kanske ni inte börjat med ännu?
Jag satte upp det i Desmos bara för att visa (för mig själv också) att teoremet jag länkade till stämmer:
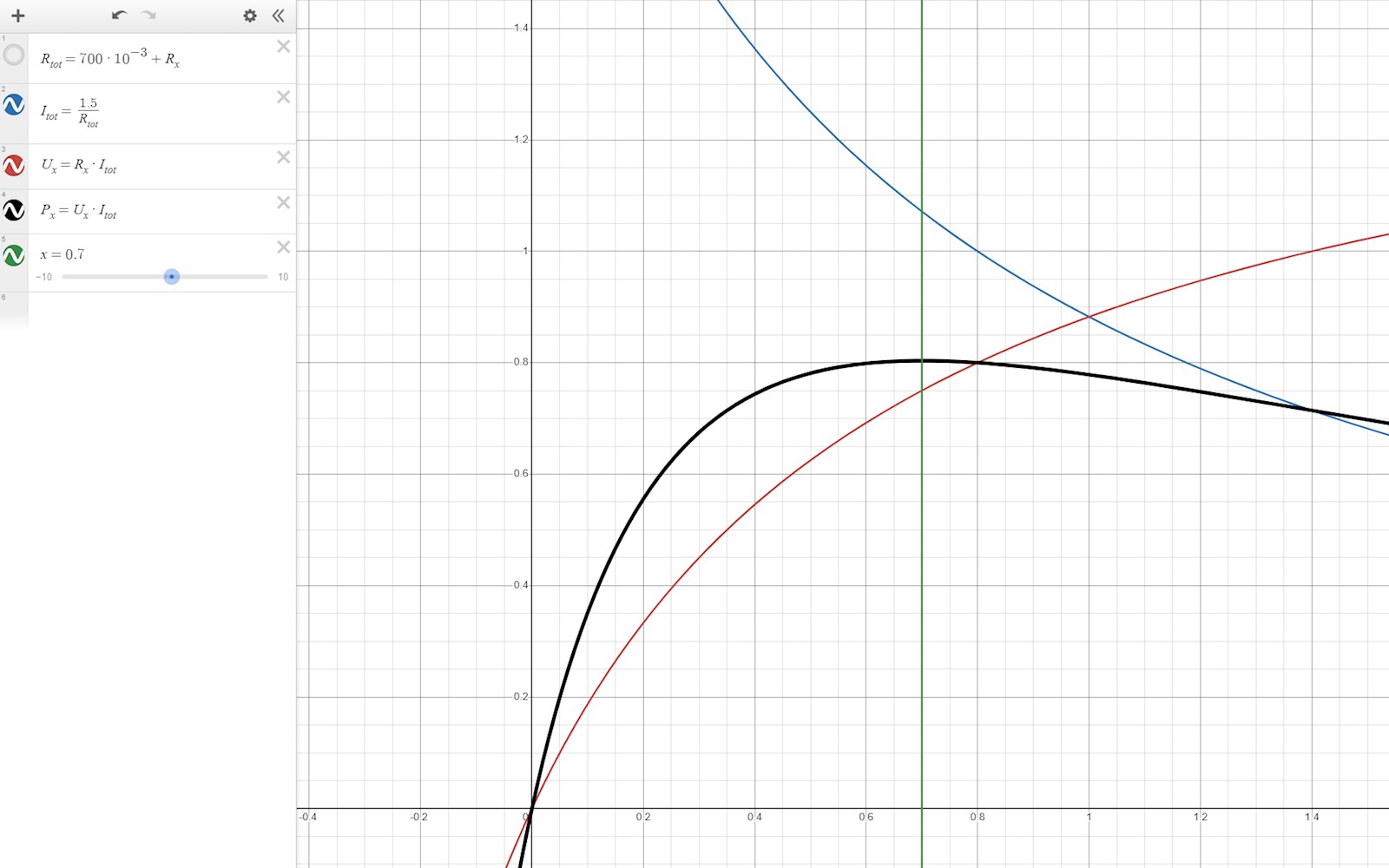
När den yttre resistansen ökar, så ökar spänningen över den, men samtidigt minskar strömmen genom den. Gröna linjen är x=700 mOhm.
Först och främst, tack för ditt svar!!
Vi har börjat med derivering (har läst t.o.m matte 4) men det ingår inte i denna kurs att integrera/derivera... Uppgifterna ska gå att lösa ändå, det var därför jag frågade. Men jag förstår inte riktigt dina grafer i bilden tyvärr (och vi får inte använda oss av dator/geogebra på kursprovet...). Men jag nöjer mig med teoremet som du nämnde. Då vet jag hädanefter att den maximala effekten fås om den yttre resistansen är lika stor som den inre (vilket stämmer enligt facit). Tack!!
Den svarta kurvan visar effekten över motståndet.
Den röda visar spänningen över det och den blå visa strömmen genom det.
I takt med att R ökar, så ökar spänningen och strömmen minskar förstås.
Den gröna linjen är R=700 mOhm, bara för att man skall kunna tycka det är rimligt att P-maximum är där.

