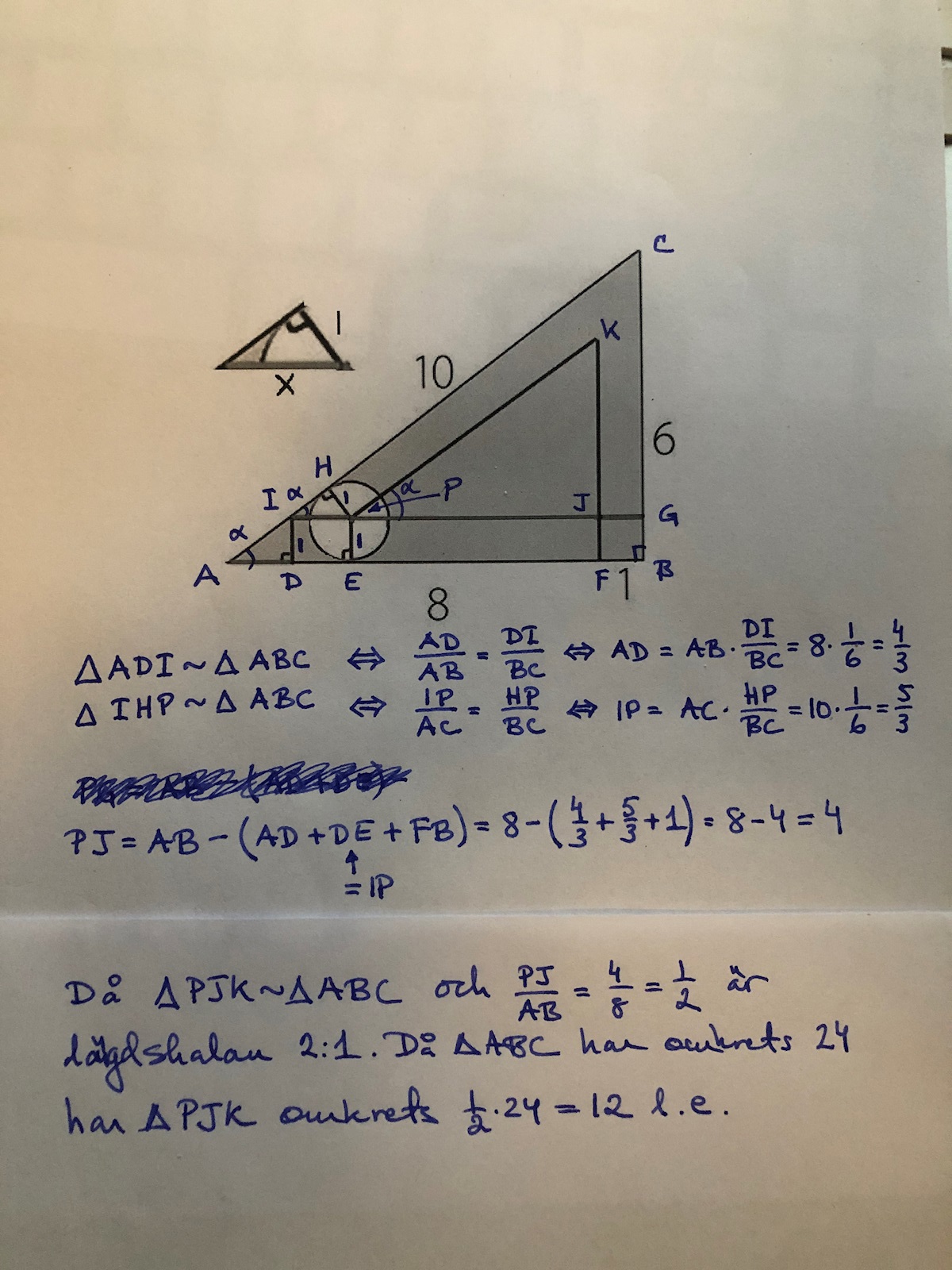
En cirkel rullar i en triangel
Hur skulle man kunna tänka här ? Tips någon ?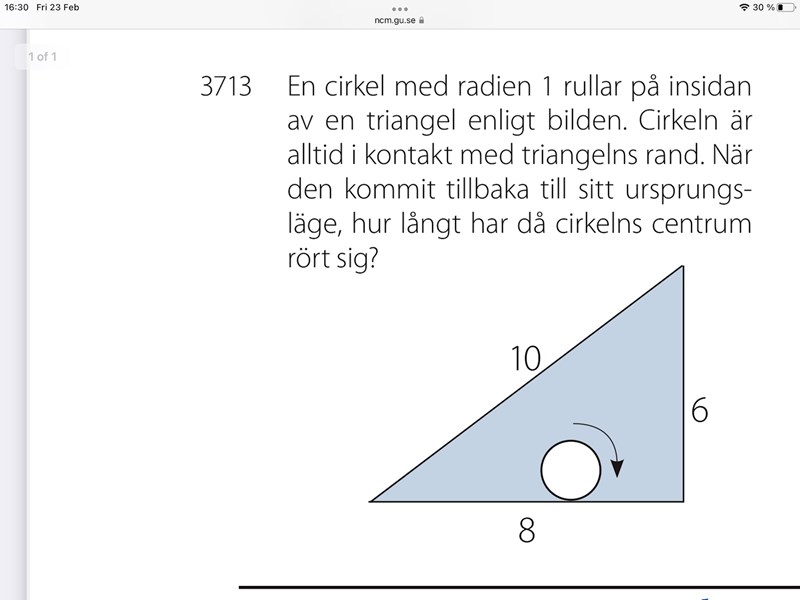
cirkelns centrum är alltid på avståndet 1 från den triangelsida den rullar på .
Rita alltså en triangel innanför den befintliga på avståndet 1 och se om du kan hitta ngt sätt att bestämma den triangelns sidor
Hur ska man tänka då ? Jag förstår ej
har du lärt dig trigonometri?
japp med rätvinkliga trianglar
Rita som jag skrev tidigare, rita även in cirkeln i ett av de spetsiga hörnen, så kan du beräkna hur långt från hörnet cirkelns kontaktpunkter med triangeln ligger.
om du kör fast, lägg upp din bild här så fortsätter vi med den som bas.
Lös gärna uppgiften med trigonometri. Sedan kan du rita så här och se att det blir något enklare utan.
Om du betänker att alla trianglarna i figuren är "egyptiska", likformiga med sidförhållandena 3:4:5.
Du behöver bara beräkna den nedre kateten i den inre triangeln, övriga ges av 3:4:5.
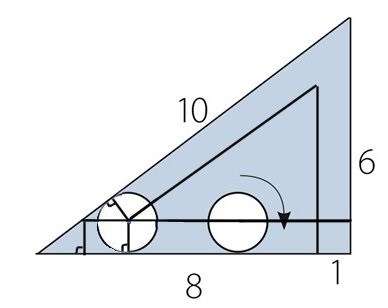
Jag förstår bara inte hur jag kan använda trigonometri i upffgiften var är det lämpligt att använda sin, cos och tan ?
Hur stor är vinkeln nere till vänster?
Rita en linje från hörnet till cirkelns mitt, den bildar med radien och nedre katetern en triangel, beräkna dess sidor (det räcker med undre katetern)
Om jag tänker rätt så behöver du inte trigonometri utan du kan använda likformiga trianglar - du har den stora triangeln, den lilla triangeln längst till höger som har cirkelns radie som sin korta katet och den ännu mindre trianglen som har cirkelns radie som sin långa katet är allihop likformiga.
Smaragdalena jag tror nog att du har rätt. Likformighet känns mer lämpligt att använda här.
Utan bilden som Louis la upp skulle jag inte ha kommit på den metoden. Louis skrev ju också att man kan lösa uppgiften utan trigonometri.
Likformighet är säkert den bästa metoden,
Synd bara att jag ännu inte kommit på hur man ska göra...
Tips: Småtrianglarna har kort katet 1. Skriv det som 3/3 så ges de andra sidorna direkt.
Louis skrev:Tips: Småtrianglarna har kort katet 1. Skriv det som 3/3 som ges de andra sidorna direkt.
Ja, nu ser även jag det! En enraderslösning!
Klart mkt enklare än att dribbla runt med tan(v) och tan(v/2)
Jag förstår bokstvligen ingenting
Den lilla röda triangeln är likformig med den stora ursprungstriangeln.
Hur lång är hypotenusan i den lilla röda?
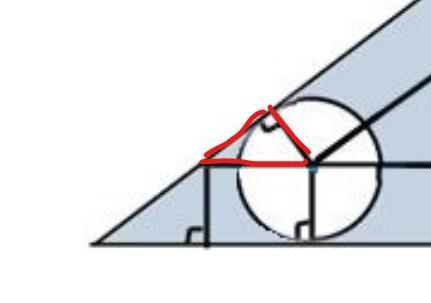
ok, då skulle vi kunna använda pythagoras. Alternativt likfromighet eller trigonometri eller ?
Men, bör vi då kalla några av triglarnas sidor x, y eller z och ställa upp et samband mha likformighet ?
Alla trianglarna i figuren är likformiga med sidförhållandena 3:4:5.
Den stora triangeln har sidorna 3*2, 4*2 och 5*2.
Den röda triangeln har kortaste sidan 1 = 3/3 ...
Ture skrev:Louis skrev:Tips: Småtrianglarna har kort katet 1. Skriv det som 3/3 som ges de andra sidorna direkt.
Ja, nu ser även jag det! En enraderslösning!
Klart mkt enklare än att dribbla runt med tan(v) och tan(v/2)
tan + tan för halva vinkeln ger en trevlig övning, men inte för Ma2 kanske.
Trinity2 skrev:Ture skrev:Louis skrev:Tips: Småtrianglarna har kort katet 1. Skriv det som 3/3 som ges de andra sidorna direkt.
Ja, nu ser även jag det! En enraderslösning!
Klart mkt enklare än att dribbla runt med tan(v) och tan(v/2)
tan + tan för halva vinkeln ger en trevlig övning, men inte för Ma2 kanske.
Jo, för en exakt lösning blir det en halv sida,
Ett närmevärde däremot tar man på två rader.
Kräver lite räkningar, visst. Likf. är nog mera avsikten här.
Jag förstår inte varför vi konstruenade två cirklar i figuren. Vet någon ?
Det är en cirkel som rullar runt. Det är när vi ritar den i hörnet, tangerad av två sidor, som vi kan räkna fram de sträckor som vi behöver. Alltså sidorna i de två små trianglarna. Den ursprungliga figurens cirkel har vi ingen användning för i räkningarna.
Har du kommit fram till svaret på Tures fråga i #17?
Jag förståe ej hur jag kan ställa upp ett förhållande mha likformighet vilka metal kan jag använda för den " röda triangeln". Vissa skrev löd uppgiften mha trigonometri tanv+tanv. Förstår icke hur det skulle hjälpa 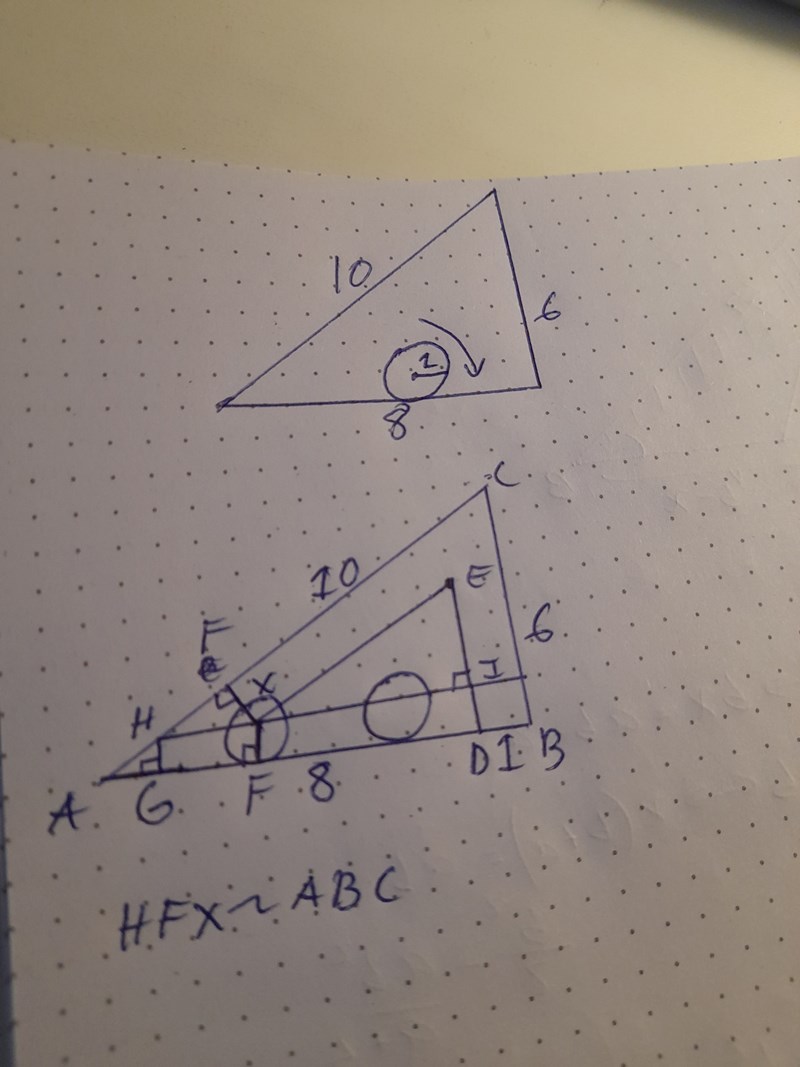
Vi går på likformigheten.
Är du med på
- att alla trianglar i figuren är likformiga med varandra?
- att alla har sidförhållandena 3:4:5 som vi får från den stora triangelns 6 cm, 8 cm och 10 cm?
- att du kan använda det på de minsta trianglarna (som är kongruenta med varandra, även om det inte ser riktigt så ut i figuren)?
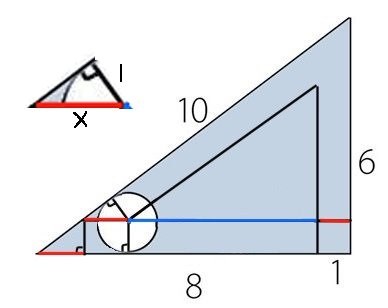
Du kan ställa upp likformighetsekvationen x/5 = 1/3, där VL gäller hypotenusor och HL kort kateter.
Det ger x = 5/3.
Jag tipsade tidigare om ett lite enklare sätt. Om du skriver 1 för kort katet i lilla triangeln som 3/3,
kan du direkt se att de andra sidorna är 4/3 och 5/3. Enligt förhållandena 3:4:5.
Där har du även lång katet i den lilla triangeln längst till vänster.
Och i och med det kan du beräkna den blåmarkerade sidan i den inre triangeln.
Är du med på att svaret på uppgiften är omkretsen av den triangeln?
neh, tyvär Louis jag förstår ej. Jag begriper däremot att alla trianglar är liformiga
Är du med på vad som menas med sidförhållanden 3:4:5?
japp det är en rätvinklig triangel enligt pythagoras sats
Vet du hur man ställer upp likformighetsekvationer när man har två likformiga trianglar?
ja men tippar på vinklarna som är motsvara varandra t ex A/A` = längdskala eller ?
Ja, i det här fallet hypotenusa i lilla/hypotenusa i stora = kort katet i lilla/kort katet i stora.
x/10 = 1/6 för att använda originalvärdena. Eller
x/5 = 1/3 om man först har gjort om 6:8:10 till 3:4:5 som är praktiskt, eftersom det förhållandet återkommer i uppgiften.
Är du med på att den röda hypotenusan är 5/3?
nej . Jag hänger inte rikitigt med på den röda hyp. är 4:3
Skrev fel först. 5/3 som lösning på ekvationen. Är du med på ekvationen?
ja
nu tänkte jag ta lite paus från matten
Ok. Om du är med på att röd hypotenusa är 5/3 och röd katet (i triangeln längst till vänster) 4/3 är det sedan mycket lite kvar.
Jag gjorde ett nytt försök och jag förstår tyvär inte hur man ska klura sig fram
Jag frågade tidigare om du arbetat med likformighet och likformighetsekvationer.
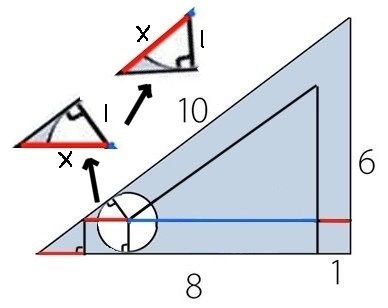
I figuren här har jag först plockat ut den lilla triangeln som vi ska bestämma.
Jag har också vänt och vridit den så att den är orienterad likadant som den stora triangeln, vars sidor vi vet.
Likformigheten ger då att
x/10 = 1/6
x = 10/6 = 5/3
Alltså att förhållandet (kvoten) mellan motsvarande sidor i de två trianglarna är detsamma vilka sidpar vi än väljer.
Kort katet i lilla triangeln är också radie i cirkeln. Och det var givet att den är 1.
Är du med på detta eller vad är du inte med på?
den här var klurig för mig
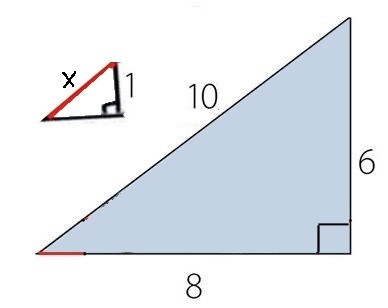
Men jag undrar fortfarande: har du räknat uppgifter som den följande?
De två trianglarna är likformiga. Beräkna x.
Ja. Men, jag blev förrivard när du hade markerat två cirklar och dragit in några fler linjer
Är det något nu som du inte är med på?
Hur lång är den andra röda sträckan som är längre katet i den lilla triangeln längst till vänster?
De små trianglarna är kongruenta med varandra. Båda har ju kort katet = 1.
Jag tyckte bara själva frågan var väldigt svår att begripa. För mig var det lite mer av logik. Jag valde frågan eftersom den var mycket annorlunda från traditionell matematik från kursboken. Frågan är tagen från nämnaren
Den andra röda sträckan går att beräkna Mha Pythagoras sats alt. Trigonometri
Men den har ju precis samma mått som triangeln vi just räknat på.
Där kort katet = 1 och hypotenusan x = 5/3.
Använd likformighet på samma sätt för att beräkna lång katet.
Du kan sätta ett y på den kateten i figuren i #42.
Ok. Jag gör mitt sista försök för dagen
Apropå att man ofta kan lösa geometriproblem på olika sätt (tråden: Hur skulle likformighet kunna användas?)
Först vill ta tillbaka vad jag sa om att likformighetsräkningen ovan är enklare än Tures ursprungliga förslag om trigonometri.
x = cot(arctan(6/8)/2) = 3 är ju enklast (snabbast) om man låter räknaren göra jobbet.
Därefter: lång (blå) katet i inre triangeln 8 - 3 - 1 = 4
Övriga sidor 3 och 5 (3:4:5-förhållandet)
Omkrets 3+4+5 = 12
Men är man inte bara ute efter ett svar utan en lösning på uppgiften, tycker jag att det är trevligare att räkna med likformighet och andra geometriska satser.
Kanske är den här varianten snyggare (mindre plottrig), inspirerad av Tures ritanvisningar:
Bisektrissatsen ger y/(6-y) = 8/10; y = 8/3 (man får visa att sträckan delar vinkeln i halvor)
Likformighet ger x/8 = 1/(8/3); x = 3
Fortsättningsvis som ovan.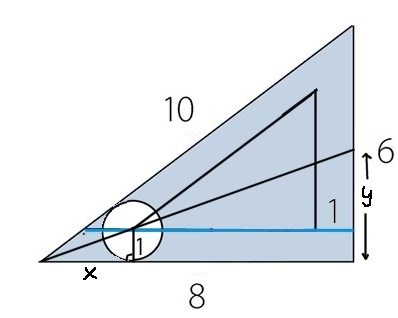
Jag har inte kommit så lång med trigonometri förutom med rätvinkligq trianglar
Och här är trianglarna rätvinkliga.
Men det finns alltså flera sätt att lösa uppgiften utan trigonometri.
Bara likformighet eller bisektrissatsen + likformighet eller ...
Hur skulle biseltris satsen har funkat ? Kan du visa
Som jag skrev (fast jag skrev fel först).
Bisektrisen delar sidan den träffar i samma förhållande
som förhållandet mellan sidorna, 8 och 10, som bildar den delade vinkeln.
Snyggt! Var hittade du lösningen?
Det var Trinity som skrev till mig på PM som jag glömde nämna. Men, förstår dessvärre inte hur Louis föreslog i #42
Arup skrev:Det var Trinity som skrev till mig på PM som jag glömde nämna.
OK försök att komma ihåg att nämna källan framöver, det hör till god ton.
Men, förstår dessvärre inte hur Louis föreslog i #42
Det jag gjorde i #40 och #42 är samma likformighet som i Trinity2:s lösning.
Ok. Jag förstår Louis
Liten tangensövning, men det finns enklare vägar…

jag begriper inget av det här. I vilken matte kurs stöter man tangens av dubbla vinklar? Och vad innebär det ens ?
Jag skulle gissa på Ma3, kanske Ma4. Det finns nog lärare här som kan ge exakt svar när det dyker upp.
Obs. Skrivfel i vänter hörn. tan(alpha/2) i täljaren! Blir rätt senare i räkningarna nedan. Slarv!
jag är nyfiken på Louis lösning i #49 skulle man använda bisektrissatsen ?
Ja, bisektrissatsen är en annan möjlighet. Känner du till den?
Bestäm y i figuren med bisektrissatsen.
Sedan x med likformighet.
jag vet inte hur man skulle kunna applicera den här.
Jag har gått igenom bisektrissatsen i skolan
Du vet alltså vad bisektrissatsen säger. Repetera annars och lös några enkla uppgifter med den.
Visa att sträckan från vinkelspetsen genom cirkelns medelpunkt är en bisektris.
Bisektrisen delar den korta kateten i delarna y och 6-y.
Sidorna som bildar den delade vinkeln är 8 och 10.
Det är allt du behöver för att kunna applicera bisektrissatsen.
Som jag gjorde i #49.
Är det något som du inte är med på?
jag vet inte hur jag skulle kunna ställa upp ett förhållande med den enligt uppgiften.
Jag fick lära mig bisektrissatsen genom att titta på vilka vinklar som motsvarar vilken sida likt likformighet.

Jag delar med mig av min tankegång imorron typ kl 20
Här har jag rensat i figuren och satt ut samma hörnbeteckningar som i dina figurer.
Det är bara att sätta in värdena i ekvationen du skrev.
Men du måste som sagt visa att AD är en bisektris.
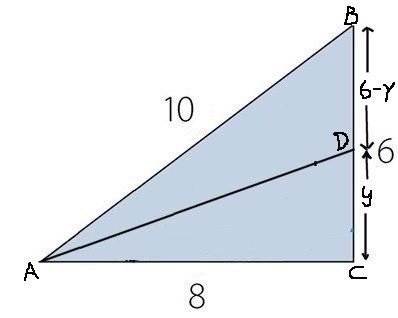
kommer det inte att då bli så här :
y6-y=81010y=48-8y18y=48⇔y=4818⇔y=83
omkretsen blir då:
O=8+83+6-83+10↔O=24
men, eftersom det är en bisektris borde väl omkretsen då bli
242=12 eller ?
Ja, y=8/3 (se #49).
Omkretsen av stora triangeln är 8 + 6 + 10 = 24, det ser man från början.
men, eftersom det är en bisektris borde väl omkretsen då bli ... 24/2 = 12
Hur tänkte du där? Bisektrisen har ingen direkt koppling med den inre triangelns storlek.
Att beräkna y var ett sätt att via likformighet komma åt x (se figuren i #49).
De fortsatta räkningarna finns i #49.
Det här sättet att lösa uppgiften är inte enklare än att bara räkna likformighet,
men jag tyckte att figuren var lite mindre plottrig utan småtrianglarna.
Och så kan det vara givande att jämföra olika lösningsmetoder.
Hej
Louis jag förstår inte vad jag gjo0rde för fel när jag tillämpade bisektrissatsen
Bisektrissatsen använde du rätt när du fick y = 8/3.
Men sedan använde du inte det resultatet alls.
Att den inre triangelns omkrets är hälften av den yttre
har ingenting med bisektrisen att göra.
Du måste fortsätta räkna som jag visade i #49.
Stens lösning:
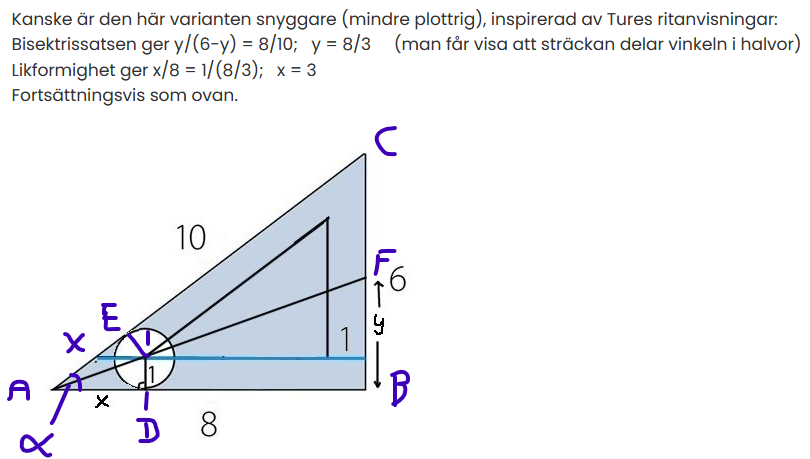
När man delar vinkeln alfa mitt itu, får man en bisektris som skär igenom cirkelns mittpunkt, när cirkeln är längst till vänster. Sträckan AD kallas x, och sträckan AE är också x lång.
Bisektrissatsen ger BF/FC = AB/AC. I vårt fall:y/(6-y) = 8/10. Vilket ger att y=8/3
Om vi kallar cirkeln mitt för P, så får vi likformighet:Triangeln ADP är likformig med triangeln ABF. I vårt fall kan det skrivas (likformighet kan uttryckas på olika sätt):x/8 = y/16x/8 = (8/3)/3. Detta ger att x=3
Om x är 3 så blir DB=5, och basen på den inre triangeln blir 8-5-1=4(vi måste ju dra bort radien när cirkeln är nederst till vänster.)
Detta ger att den inre, mindre, triangeln får sidor som är hälften av längden av den yttre triangeln ABC. Alltså 4+3+5 = 12.

- 15:25 – 28 minuter sedan
8-5-1 = 4?
oj svaret blir 2
oj svaret blir 2
Svaret blir 4, för du menade inte 8-5-1 utan 5-1. Eller 8-3-1 om vi backar ett steg.
Med den rättelsen har du en komplett lösning.
Stens lösning:
Sten har inte skrivit tidigare i tråden. Hur kom han in i bilden?
Ja frågade han på livestream om hur de menade med biskterissatsen på #49
Ok, det är bra om du nämner sådant, annars kan det bli förvirrande.
En kompletterande variant.

Jan Ragnar skrev:En kompletterande variant.
Jag förstår inte hur du menar
Så bra!