En damm med gift (differentialekvation)
Hej! Jag har fastnat på följande uppgift 3327 från Ma5000
Hur ska jag tänka? Både i generella fallet och detta specifika. Jag vet inte riktigt hur jag tänker, men har påbörjat försök på en lösning, vilken dock är felaktig..
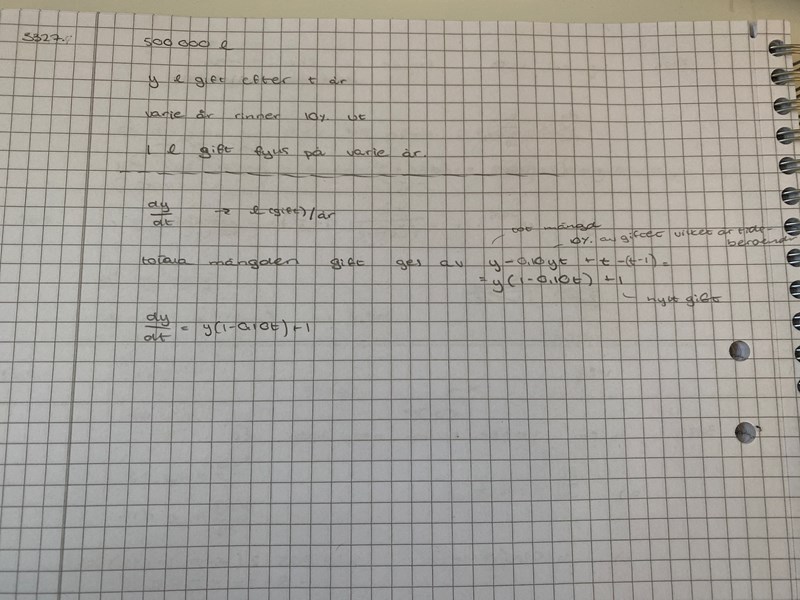
y(t) = antal liter gift efter t år. Då är y'(t) förändringen i antal liter gift per år. Giftet flödar både in i och ut ur dammen, så dela upp förändringen i två delar:
y'(t) = (antal liter gift IN i dammen under året) - (antal liter gift UT ur dammen under året)
Dessa kan undersökas separat. Hur mycket gift flödar in i dammen på ett år? Och hur mycket flödar ut (lite svårare)? I din lösning har du skrivit "1 l gift fylls på varje år", och det ser rätt ut. Ekvationen kan alltså redan förenklas till
y'(t) = 1 - (antal liter gift UT ur dammen under året)
Du har också skrivit "varje år rinner 10y ut". Det låter suspekt. Det kan inte vara mängden gift du pratar om, för dammen innehåller bara y liter gift, så det kan inte rinna ut 10y liter gift. Men om det är volymen vatten du menar, då har du antagit att det som rinner ut alltid är 10 % gift. Det vet vi inte! Det som står är att en tiondel av dammens vatten rinner ut, vilket är 500 000 / 10 = 50 000 liter, och det är en blandning av gift och rent vatten i någon proportion.
Det vår ekvation behöver veta är hur många liter *gift* som rinner ut, har du en idé hur vi kan hitta det?
Det står dock att vi ska anta att giftet är jämt fördelat i sjön, och därmed rinner 10% ut varje år. Jag skrev 0,10 och inte 10, men det blev nog lite slarvigt.. ;)
Du har också skrivit "varje år rinner 10y ut". Det låter suspekt. Det kan inte vara mängden gift du pratar om, för dammen innehåller bara y liter gift, så det kan inte rinna ut 10y liter gift. Men om det är volymen vatten du menar, då har du antagit att det som rinner ut alltid är 10 % gift. Det vet vi inte! Det som står är att en tiondel av dammens vatten rinner ut, vilket är 500 000 / 10 = 50 000 liter, och det är en blandning av gift och rent vatten i någon proportion.
Det var det här jag pratade om:
Där står väl 10y ganska tydligt? Men ja, vi är överens om att giftet är jämt fördelat och att 10 % av giftet rinner ut varje år. Så ut åker 0.10y liter gift varje år. Sätt in det i ekvationen:
y'(t) = 1 - 0.10y
Skaft skrev:Det var det här jag pratade om:
Där står väl 10y ganska tydligt? Men ja, vi är överens om att giftet är jämt fördelat och att 10 % av giftet rinner ut varje år. Så ut åker 0.10y liter gift varje år. Sätt in det i ekvationen:
y'(t) = 1 - 0.10y
Aha, då hänger jag med :) Tack så supermycket :)
