En fabrik producerar en vara där produktionskostnaden i kronor per producerad...
Hejsan! Jag är osäker på om jag har gjort denna uppgiften korrekt. På grund av det så behöver jag ocksp hjälp med c delen.
Så här lyder frågan:
En fabrik producerar en vara där produktionskostnaden i kronor per producerad enhet kan modelleras med funktionen
där x är antal producerade enheter (i hundratal).
a) Bestäm hur kostnaden förändras när produktionen ökar.
b) För vilken produktionsmängd är kostnaden som lägst?
c) Tolka svaret i b) i en verklig kontext. Vad innebär det för fabriken?
Motivera alla dina svar med både beräkningar och förklaringar.
Mitt svar:
a) Vi tar reda på förändringshastigheten genom att ta derivatan av funktionen
K(x)=200x−0.5x2 + 300
K′(x)=200−(2 ⋅ 0.5x2) + 0
K′(x)=200−x
Derivatan representerar marginalkostnaden. x är produktionen.
Om x är större än 200 så kommer kostnaden att sänka
Till exempel, x = 220
K' (220) = 200 - 220 = -20kr
Om x är mindre än 200 så kommer kostnaden att öka
Till exempel, x = 50
K' (50) = 200 - 50 = 150kr
b) Den lägsta möjliga produktionen skulle vara 0
Det betyder att x = 0
K' (0) = 200 - 0 = 200kr
Även om inget produceras så behöver fabriken betala 200kr.
Tack!
Är kostnaden 0 om man tillv ca 400?
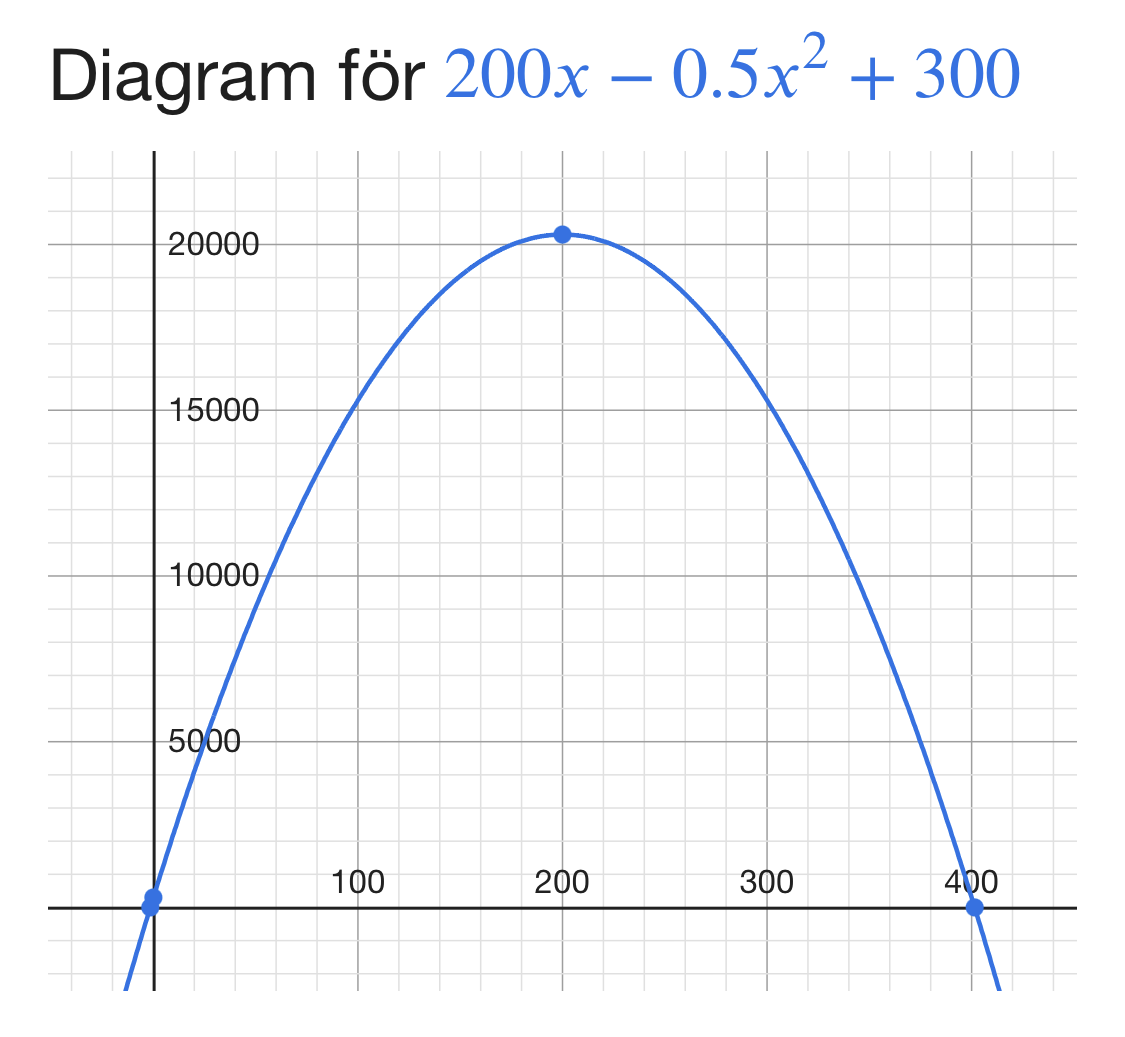
Det var produktionen som skulle vara 0, inte kostnaden. Är det inte korrekt?
Jag förstår ej modellen om kostnaden är 0.
Om funktionen verkligen representerar produktionskostnaden [kr / 100enheter], så är modellen väldigt orimlig.
Modellen innebär att företaget tjänar pengar på själva tillverkningen (d.v.s. utan att sälja något) ifall de producerar mer är x=400, d.v.s. mer än 40000 enheter. Något sådant är verklighetsfrånvänt på riktigt.
Har någon detalj försvunnit från uppgiftens frågeställning? Kan du visa bilden på hela uppgiften?
Jag kände också att den var lite orimlig men jag tänkte att det var okej eftersom den är en påhittad fråga. Det här är hela frågan, det finns inget mer till den.
Jag skulle plotta den totala produktionskostnaden xK(x) och intressera mig för när den är störst. Bortom den punkten är modellen orimlig, för då blir det billigare att producera för många saker och kasta bort en del av dem.
saffa.k07 skrev:Jag kände också att den var lite orimlig men jag tänkte att det var okej eftersom den är en påhittad fråga. Det här är hela frågan, det finns inget mer till den.
Det är alltså inte något från en bok, utan något du har konstruerat själv?
Den är en fråga från ett uppdrag, jag går på Hermods Distansgymnasium
saffa.k07 skrev:Den är en fråga från ett uppdrag, jag går på Hermods Distansgymnasium
Det är ett mysterium.
LuMa07 skrev:Modellen innebär att företaget tjänar pengar på själva tillverkningen (d.v.s. utan att sälja något) ifall de producerar mer är x=400, d.v.s. mer än 40000 enheter. Något sådant är verklighetsfrånvänt på riktigt.
De kanske är falskmyntare!
Jag känner att det blir lite utanför ämnet här😅. Jag kände allt blev enklare när jag tog derivatan eftersom vi vill veta kostnadens förändringshastighet och gå utifrån det senare visst?



