En fråga kring fjäderkonstanten k och en annan konstant

 I dina tabeller ser det ut som att den längd som du mätt minskar med kraften. Vilken längd står i tabellen, inte fjäderns längd antar jag? Rita en figur då förstår man bättre vilken slags längd du har mätt.

Proportionalitetskonstanten k=F/y måste ha enheten [N/m], dvs hur många Newton som krävs för att dra ut fjädern 1m. Hur avläser du då k ur din tabell?

Fråga 2. Jag förstår din förvirring. Lätt att blanda ihop olika jämviktslägen. Det är jämviktsläget _före_ du applicerar den nya kraften, som du ska mäta ifrån.

JohanF skrev:

 I dina tabeller ser det ut som att den längd som du mätt minskar med kraften. Vilken längd står i tabellen, inte fjäderns längd antar jag? Rita en figur då förstår man bättre vilken slags längd du har mätt.

Hej igen. Ursäkta mig! Det var ett skrivfel *facepalm*.  Tabellerna ska se ut så här, och "Längd (m)" är längden på fjädern:

fjäder 1

Belastning (N)           Längd (m) 

  0 N                                0,21 m

  1,0 N                             0,30 m

  2,0 N                             0,39 m

  3,0  N                            0,48 m

fjäder 2

Belastning (N)          längd (m)   

    0 N                           0,29 m

    1,0 N                       0,52 m

    2,0 N                       0,75 m

JohanF skrev:

Proportionalitetskonstanten k=F/y måste ha enheten [N/m], dvs hur många Newton som krävs för att dra ut fjädern 1m. Hur avläser du då k ur din tabell?

Okej, så $k$ har enheten $N/m$, vilket betyder hur många Newton som krävs för att dra fjädern $1,0 m$...  för att då erhålla $k$ ur, låt säga, tabell 1, måste jag kanske iaktta ett mönster. Detta mönster tror jag är att för varje Newton så förlängs fjädern med $0,09 m$. 

 $y =\hspace{0.17em}0,09 \times 11 = 0,99 m [ungefär en meter]$. $F_k = 11 N$.  $k = \frac{F_k}{y} = \frac{11}{0,99} = \frac{100}{9} N/m.$

Är det kanske detta jag ska avläsa? Det känns som att jag förmodligen krånglar till det eller missar något väldigt enkelt :/

JohanF skrev:

Fråga 2. Jag förstår din förvirring. Lätt att blanda ihop olika jämviktslägen. Det är jämviktsläget _före_ du applicerar den nya kraften, som du ska mäta ifrån.

Detta har jag lite svårt att hänga med på... Menar du här att man för varje vikt ska man dokumentera fjäderkonstanten, för då får man t.ex. fyra olika jämviktslägen: 0,21 m, 0,30 m, 0,39 m och 0,48 m --- och detta känns svårhanterligt.  Eller menar du att man ska anta att jämviktsläget är när N = 0, dvs. fjädern innan belastning?

Tack!

Du tänker helt rätt angående mönstret, men du gör det lite krångligt för dig. Det enklaste och bästa sättet att uppskatta proportionalitetskonstanten är ju att plotta dina värden i en graf. (Kraften på y-axeln och elongationen på x-axeln) och sedan beräkna lutningskoefficienten på linjen.

Det blir som sagt lite förvirrande att prata om jämviktsläge i den typen av mätning du utförde. Som du ser i figuren nedan så kan Hookes lag stämma sämre då man närmar sig extremvärden på elongationen (stor kompression eller stor förlängning, den streckade linjen). Därför vill man gärna mäta k när man gör en utdragning ifrån ett läge där fjädern redan är "normalbelastad". Det är denna grundbelastning som man kallar jämvikt. Tex om man hänger en 100g vikt i fjädern (dvs ca1N), och kallar detta för jämviktsläge. Sedan dra i vikten ytterligare 1N för att se hur mycket elongationen ökar ifrån jämviktsläget. I dina mätningar så ser det inte ut att spela någon roll eftersom mätningarna ger samma resultat om du drar ut fjädern 1N extra ifrån obelastad fjäder eller om du drar ut fjädern 1N extra då fjädern redan är belastad med 1N.      

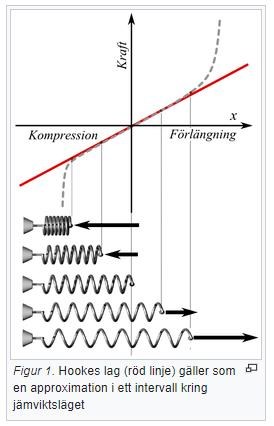
Det är pga denna eventuella ickelinjäritet (avvikelse från Hookes lag) när fjädern är långt ifrån jämviktsläget som man kan upptäcka om man plottar sina mätvärden i en graf, och har då möjlighet att exkludera extrempunkter som inte ser ut att passa in i k-värdet för fjäderns linjära område.   

Så, tillbaka till din fråga. Ja, jämviktsläget skulle kunna vara vid obelastad fjäder, men det skulle också kunna ligga någonannanstans. Det beror på konstruktionen av fjädern. Din fjäder ser ut att fungera med ett obelastad fjäder som jämviktsläge.

JohanF skrev:

Du tänker helt rätt angående mönstret, men du gör det lite krångligt för dig. Det enklaste och bästa sättet att uppskatta proportionalitetskonstanten är ju att plotta dina värden i en graf. (Kraften på y-axeln och elongationen på x-axeln) och sedan beräkna lutningskoefficienten på linjen.

 

Det blir som sagt lite förvirrande att prata om jämviktsläge i den typen av mätning du utförde. Som du ser i figuren nedan så kan Hookes lag stämma sämre då man närmar sig extremvärden på elongationen (stor kompression eller stor förlängning, den streckade linjen). Därför vill man gärna mäta k när man gör en utdragning ifrån ett läge där fjädern redan är "normalbelastad". Det är denna grundbelastning som man kallar jämvikt. Tex om man hänger en 100g vikt i fjädern (dvs ca1N), och kallar detta för jämviktsläge. Sedan dra i vikten ytterligare 1N för att se hur mycket elongationen ökar ifrån jämviktsläget. I dina mätningar så ser det inte ut att spela någon roll eftersom mätningarna ger samma resultat om du drar ut fjädern 1N extra ifrån obelastad fjäder eller om du drar ut fjädern 1N extra då fjädern redan är belastad med 1N.      

Det är pga denna eventuella ickelinjäritet (avvikelse från Hookes lag) när fjädern är långt ifrån jämviktsläget som man kan upptäcka om man plottar sina mätvärden i en graf, och har då möjlighet att exkludera extrempunkter som inte ser ut att passa in i k-värdet för fjäderns linjära område.   

 

Så, tillbaka till din fråga. Ja, jämviktsläget skulle kunna vara vid obelastad fjäder, men det skulle också kunna ligga någonannanstans. Det beror på konstruktionen av fjädern. Din fjäder ser ut att fungera med ett obelastad fjäder som jämviktsläge.

Tack så himla mycket! Nu känns det som jag är på spåren! Det enda jag inte minns hur man gjorde var inmatning av värden i en online-graf XD. Det är väl så att man går till en hemsida, t.ex. Desmos, och skriver ungefärligen: (0.21, 0), (0.30, 1) och så vidare samt sist beräkna k-värdet för funktionen? Syntaxen sätter stop för mig :/

Edit: så när jag får fram k-värdet för bägge fjädrar,  tänkte jag beräkna fjäderkonstanten för dem med jämviktsläget där F = 0. Då har jag visat att kraften är proportionell mot förlängningen i och med beräkningen av k-värdet; också får jag ut en godtycklig siffra på fjäderkonstanten med F = 0 som utgångspunkt. Sedan borde jag vara klar!

RandigaFlugan skrev:

JohanF skrev:

Du tänker helt rätt angående mönstret, men du gör det lite krångligt för dig. Det enklaste och bästa sättet att uppskatta proportionalitetskonstanten är ju att plotta dina värden i en graf. (Kraften på y-axeln och elongationen på x-axeln) och sedan beräkna lutningskoefficienten på linjen.

 

Det blir som sagt lite förvirrande att prata om jämviktsläge i den typen av mätning du utförde. Som du ser i figuren nedan så kan Hookes lag stämma sämre då man närmar sig extremvärden på elongationen (stor kompression eller stor förlängning, den streckade linjen). Därför vill man gärna mäta k när man gör en utdragning ifrån ett läge där fjädern redan är "normalbelastad". Det är denna grundbelastning som man kallar jämvikt. Tex om man hänger en 100g vikt i fjädern (dvs ca1N), och kallar detta för jämviktsläge. Sedan dra i vikten ytterligare 1N för att se hur mycket elongationen ökar ifrån jämviktsläget. I dina mätningar så ser det inte ut att spela någon roll eftersom mätningarna ger samma resultat om du drar ut fjädern 1N extra ifrån obelastad fjäder eller om du drar ut fjädern 1N extra då fjädern redan är belastad med 1N.      

Det är pga denna eventuella ickelinjäritet (avvikelse från Hookes lag) när fjädern är långt ifrån jämviktsläget som man kan upptäcka om man plottar sina mätvärden i en graf, och har då möjlighet att exkludera extrempunkter som inte ser ut att passa in i k-värdet för fjäderns linjära område.   

 

Så, tillbaka till din fråga. Ja, jämviktsläget skulle kunna vara vid obelastad fjäder, men det skulle också kunna ligga någonannanstans. Det beror på konstruktionen av fjädern. Din fjäder ser ut att fungera med ett obelastad fjäder som jämviktsläge.

Tack så himla mycket! Nu känns det som jag är på spåren! Det enda jag inte minns hur man gjorde var inmatning av värden i en online-graf XD. Det är väl så att man går till en hemsida, t.ex. Desmos, och skriver ungefärligen: (0.21, 0), (0.30, 1) och så vidare samt sist beräkna k-värdet för funktionen (dvs. fjäderkonstanten)? Syntaxen sätter stop för mig :/

Fixa en ny tråd med din fråga, jag kan inte det där. Jag brukar använda excel och trendline equation.

JohanF skrev:

RandigaFlugan skrev:

Visa föregående citat

JohanF skrev:

Du tänker helt rätt angående mönstret, men du gör det lite krångligt för dig. Det enklaste och bästa sättet att uppskatta proportionalitetskonstanten är ju att plotta dina värden i en graf. (Kraften på y-axeln och elongationen på x-axeln) och sedan beräkna lutningskoefficienten på linjen.

 

Det blir som sagt lite förvirrande att prata om jämviktsläge i den typen av mätning du utförde. Som du ser i figuren nedan så kan Hookes lag stämma sämre då man närmar sig extremvärden på elongationen (stor kompression eller stor förlängning, den streckade linjen). Därför vill man gärna mäta k när man gör en utdragning ifrån ett läge där fjädern redan är "normalbelastad". Det är denna grundbelastning som man kallar jämvikt. Tex om man hänger en 100g vikt i fjädern (dvs ca1N), och kallar detta för jämviktsläge. Sedan dra i vikten ytterligare 1N för att se hur mycket elongationen ökar ifrån jämviktsläget. I dina mätningar så ser det inte ut att spela någon roll eftersom mätningarna ger samma resultat om du drar ut fjädern 1N extra ifrån obelastad fjäder eller om du drar ut fjädern 1N extra då fjädern redan är belastad med 1N.      

Det är pga denna eventuella ickelinjäritet (avvikelse från Hookes lag) när fjädern är långt ifrån jämviktsläget som man kan upptäcka om man plottar sina mätvärden i en graf, och har då möjlighet att exkludera extrempunkter som inte ser ut att passa in i k-värdet för fjäderns linjära område.   

 

Så, tillbaka till din fråga. Ja, jämviktsläget skulle kunna vara vid obelastad fjäder, men det skulle också kunna ligga någonannanstans. Det beror på konstruktionen av fjädern. Din fjäder ser ut att fungera med ett obelastad fjäder som jämviktsläge.

Tack så himla mycket! Nu känns det som jag är på spåren! Det enda jag inte minns hur man gjorde var inmatning av värden i en online-graf XD. Det är väl så att man går till en hemsida, t.ex. Desmos, och skriver ungefärligen: (0.21, 0), (0.30, 1) och så vidare samt sist beräkna k-värdet för funktionen (dvs. fjäderkonstanten)? Syntaxen sätter stop för mig :/

Fixa en ny tråd med din fråga, jag kan inte det där. Jag brukar använda excel och trendline equation.

Okej! Jag tror jag kommer lära mig det där med grafen själv. Tack för all din hjälp! Jag säger till om en ny fundering dyker upp om fjädern. :)