En kloss med massan 2,5kg hänger i en fjäder. (Svängningsenergi-uppgift)
En kloss med massan 2,5kg hänger i en fjäder. Klossen lyfts sedan rakt upp till höjden då kraften från fjädern blir noll och släpps. Vilken är kraften från fjädern på klossen då den befinner sig i rörelsen nedersta punkt.
Jag tänker att man ska använda sig av Hookes lag för att räkna ut kraften men då saknas både fjäderkonstanten och delta l, så hur tar jag reda på vad det är för nedesta höjd?
komplettera din bild med klossens läge i sitt nedersta läge efter det att du släppt klossen.
Inför lite beteckningar för nedersta läget och jämnviktsläget.
Sen kan du vara mogen att sätta upp
Hooks lag för
och göra en energibetraktelse.
Titta på hur energin flyttas från lägesenergi till rörelseenergi och i fjädern lagrad energi
Sätt upp sambandet för energiomvandlingen och har du gjort rätt så kommer det i slutändan enbart att återstå en konstant och mg.
Lägg upp bilden med beteckningar här och också hur långt du räknat om du behöver ytterligare hjälp.
Förstår fortfarande inte riktigt, i nedersta läget kommer potentiella energin vara 0 och rörelseenergin som högst men jag vet fortfarande för lite.
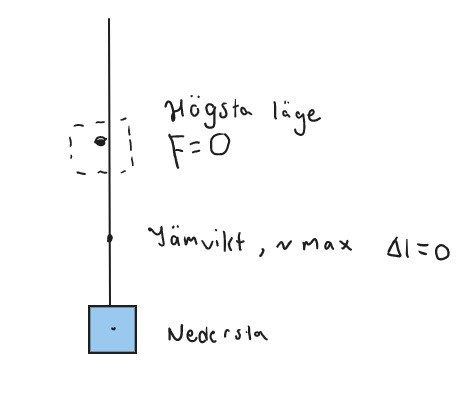
i nedersta läget står klumpen still och rörelseenergin är....?
Ture skrev:i nedersta läget står klumpen still och rörelseenergin är....?
Aa så då är rörelseenergin 0 och den potentiella energin 0?
Det beror på var du lagt din nollnivå.
Jag föreslår att du lägger nollnivån där klumpen vänder efter släpp, i så fall är lägesenergin 0 där.
Hur ser Hooks lag i ursprungsläget, med dina beteckningar?
Hur ser energisambandet ut i nedre vändläget med dina beteckningar?
Ture skrev:Det beror på var du lagt din nollnivå.
Jag föreslår att du lägger nollnivån där klumpen vänder efter släpp, i så fall är lägesenergin 0 där.
Hur ser Hooks lag i ursprungsläget, med dina beteckningar?
Hur ser energisambandet ut i nedre vändläget med dina beteckningar?
Hookes lag: F=k·∆l
Ek=0 Ep= k·(∆l)22
Etot= k·A22
Men jag vet ej vad varken k,l ,Feller A har för värden
Axiom skrev:Ture skrev:Det beror på var du lagt din nollnivå.
Jag föreslår att du lägger nollnivån där klumpen vänder efter släpp, i så fall är lägesenergin 0 där.
Hur ser Hooks lag i ursprungsläget, med dina beteckningar?
Hur ser energisambandet ut i nedre vändläget med dina beteckningar?
Hookes lag: F=k·∆l
Ek=0 Ep= k·(∆l)22
Etot= k·A22
Men jag vet ej vad varken k,l ,Feller A har för värden
Det blir lättare för dig om du i din figur inför alla beteckningar du använder, annars gör man lätt fel. (Det blir lättare för mig med)
Jag kallar fjäderns utdragning för x, nedersta läget för l, fjäderkonstanten för k och startläget för ∆l .
För energin gäller, i godtyckligt utdragningsläge för fjädern, under rörelsen:
mg(∆l) = mv2/2 + kx2/2
i nedersta läget alltså
1: mg(∆l) = kl2/2
i ursprungsläget vet vi att på klumpen verkar två krafter, mg och fjäderkraften, Hooks lag ger då:
2: mg = k(∆l)
Kraften från fjädern i nedersta läget får vi med Hooks lag igen
3: F = k*l
Med 1,2 och ekv 3 kan du lösa ut F
Ture skrev:Axiom skrev:Ture skrev:Det beror på var du lagt din nollnivå.
Jag föreslår att du lägger nollnivån där klumpen vänder efter släpp, i så fall är lägesenergin 0 där.
Hur ser Hooks lag i ursprungsläget, med dina beteckningar?
Hur ser energisambandet ut i nedre vändläget med dina beteckningar?
Hookes lag: F=k·∆l
Ek=0 Ep= k·(∆l)22
Etot= k·A22
Men jag vet ej vad varken k,l ,Feller A har för värden
Det blir lättare för dig om du i din figur inför alla beteckningar du använder, annars gör man lätt fel. (Det blir lättare för mig med)
Jag kallar fjäderns utdragning för x, nedersta läget för l, fjäderkonstanten för k och startläget för ∆l .
För energin gäller, i godtyckligt utdragningsläge för fjädern, under rörelsen:
mg(∆l) = mv2/2 + kx2/2
i nedersta läget alltså
1: mg(∆l) = kl2/2
i ursprungsläget vet vi att på klumpen verkar två krafter, mg och fjäderkraften, Hooks lag ger då:
2: mg = k(∆l)
Kraften från fjädern i nedersta läget får vi med Hooks lag igen
3: F = k*l
Med 1,2 och ekv 3 kan du lösa ut F
Men det är väl bara en av ekvationerna som innehåller F ?
Jovisst, men du måste använda de andra två ekvationerna för att bli av med de okända k och l i den ekvationen!
Uppgiften var betydligt mycket enklare än vad jag först trodde. Där kraften är 0 har vikten dragits ut en längd, x och där är kraften mg=k*x
I nedersta läget har den dragits ut k*2x=2mg
Axiom skrev:Uppgiften var betydligt mycket enklare än vad jag först trodde. Där kraften är 0 har vikten dragits ut en längd, x och där är kraften mg=k*x
I nedersta läget har den dragits ut k*2x=2mg
2mg är rätt.


