En ränna med lodräta sidor
"Av fyra lika brädor vill man göra en ränna med lodräta sidor. Vilken vinkel skall bottenbrädorna bilda med varandra för att rännan skall rymma så mycket som möjligt?"
Jag sätter längden på brädorna till 1 för enkelhetens skull.
Sedan skriver jag ett uttryck för arean.
När jag sedan deriverar arean, vilket jag gör i Wolfram Alpha för att jag är lat, och sedan säger att derivatan skall vara 0, då blir det inte rätt svar. Så jag tror jag gör nåt fel. Men vore tacksam om någon kan titta ifall jag har gjort nåt fel redan här.
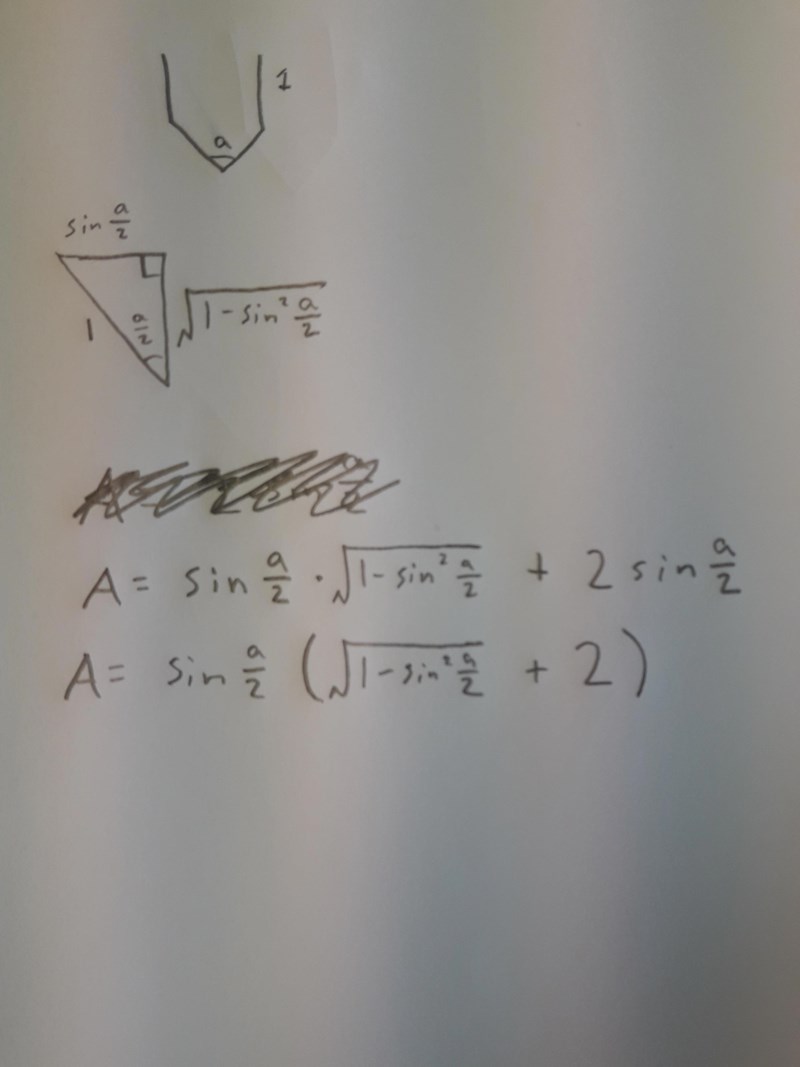
Edit: Ser rätt ut :-)
Vad kommer Wolfram Alpha fram till?
180 grader.
Jag får inte Wolfram att svara 180 grader hur jag än gör. Det känns lite komplicerat att uttrycka "höjden" som sqrt(1-(sin(a/2)^2)). Om du istället använder cos(a/2) så blir det lättare att derivera på egen hand.
Kanske nåt parentesfel. Kan du ta en bild av hur det ser ut i Wolfram Alpha när du får 180 grader?
Jag kör på tipset från Mega7853 och skriver höjden som cos(a/2) istället.
A = sin(a/2) * (cos(a/2) + 2)
A' = 1/2 (cos(a/2) (cos(a/2) + 2) - sin^2(a/2))
1/2 (cos(a/2) (cos(a/2) + 2) - sin^2(a/2)) = 0
((cos(a/2))^2 + 2cos(a/2))/2 = (sin(a/2))^2
Är det bara att börja använda några slags trigonometriska formler för att lösa detta nu?
Ja, om man först använder några trigonometriska likheter så kan man sedan få det till en andragradsekvation efter en substitution. Man löser andragradsekvationen, väljer den lämpliga av lösningarna och löser ut vinkeln ur substitutionen. Klart!
Trigonometriska ettan blev bra. Tusen tack!




