En term fel i logarithmering av Likelihoodfunktion

Hej. Jag arbetade lite med denna uppgiften

har en fråga kring b) specifikt.

Jag får fram samma skattning som facit gör i slutändan, men jag får termen $\frac n \gamma$

I a)-uppgiften får man följande resultat

sen använder man det för att ta fram Likelihood (och Log-likelihood)-funktionen i b)

Men det har väl blivit något knas när jag själv har fått fram $\ln L(\gamma)$ då jag får att den sista termen ser lite annorlunda ut. Kan inte hitta vad som är fel.

Jag får att

$L(\gamma) = \frac 1 {y^n} \prod_{i=1}^{i=n} y_i^{1/\gamma-1}$

$\ln L(\gamma) = \ln (\frac 1 {y^n} \prod_{i=1}^{i=n} y_i^{1/\gamma-1})$

$=\ln(1)-n\ln(y)+\ln(\prod_{i=1}^{i=n} y_i^{1/\gamma-1})$

termen $\ln(\prod_{i=0}^{i=n} y_i^{1/\gamma-1})$ får jag till

$\ln(\prod_{i=1}^{i=n} y_i^{1/\gamma-1})=$

$\sum_{i=1}^{i=n} \ln(y_i^{1/\gamma-1})$

$\sum_{i=1}^{i=n} (\frac 1 \gamma - 1) \cdot \ln(y_i)$

eftersom termerna "adderas" $n$ gånger flyttar jag ut $\frac 1 \gamma$

dvs

$ln(\prod_{i=0}^{i=n} y_i^{1/\gamma-1})$

$=(\frac n \gamma - 1) \sum_{i=1}^{i=n} ln(y_i)$

men om man kikar på facit så har de inte fått $(\frac n \gamma - 1)$ utan $(\frac 1 \gamma - 1)$ framför summan:

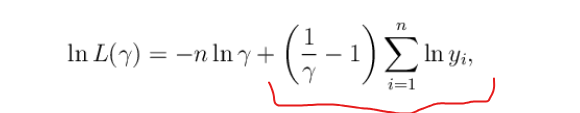
antar att det bara är nåt simpel sak jag gjort fel på som jag inte hittar.

Hjälp uppskattas!