Energiresonemang
Hej! Jag skulle vilja lösa uppgiften nedan med energiresonemang (Ek=Ep) men hur får jag med friktionsarbetet i det? 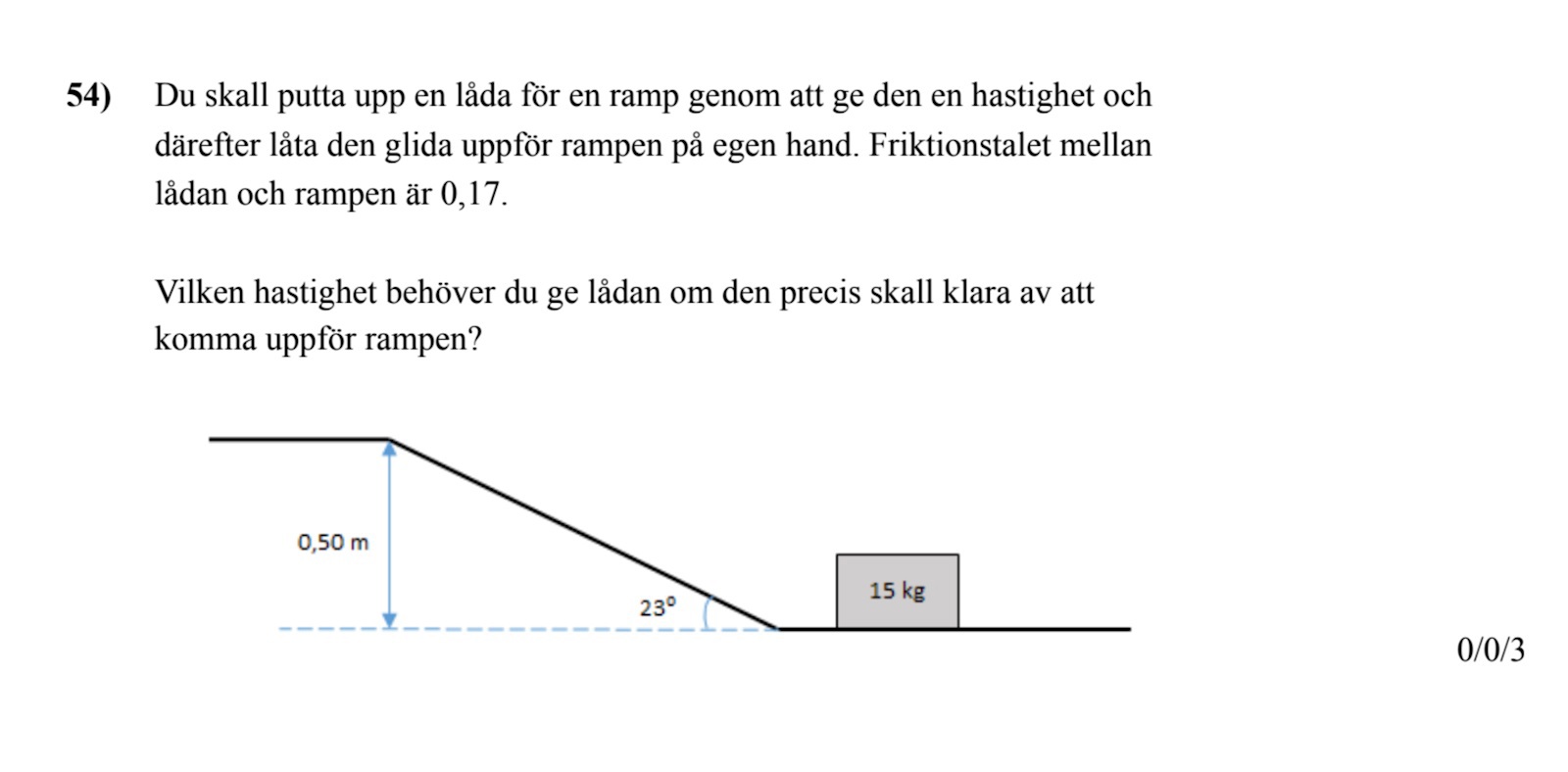
Vad är kraften på lådan på det lutande planet?
Menar du kraftresultanten?
Då är det friktionskraften+tyngdkraftens x-komposant.
Men jag vill ju använda ett energiresonemang?
Vi kommer till det senare
Skriv ett uttryck för friktionskraften + gravitationskomponsanten
mgcos67+0.17mgsin23 ?
Vart kommer 67 ifrån
Och sedan blandar du ihop sin och cos
Mg cos x - normalkraften
Fungerar det att tänka att cos(180-90-23=67)=F_x/mg => x-komposanten=mgcos67?
ItzErre skrev:Vart kommer 67 ifrån
Och sedan blandar du ihop sin och cos
Mg cos x - normalkraften
Tänker nog 90-23=67.
Men som du säger är det mg*cos(23) som gäller för N (vinkelrät mot lutningen).
cforsberg skrev:ItzErre skrev:Vart kommer 67 ifrån
Och sedan blandar du ihop sin och cos
Mg cos x - normalkraften
Tänker nog 90-23=67.
Men som du säger är det mg*cos(23) som gäller för N (vinkelrät mot lutningen).
Varför fungerar inte det andra sättet? Visserligen mycket krångligare, men ändå? :/
Slå in cos (67) och cos (23) på en Miniräknare
Så att jag förstår det rätt: det ska vara mgsin23 som är x-komposanten? För i sådant fall kan ju x-komposanten också skrivas mgcos67
Majskornet skrev:Så att jag förstår det rätt: det ska vara mgsin23 som är x-komposanten? För i sådant fall kan ju x-komposanten också skrivas mgcos67
Ja. Vad är definitionen av sin? Jo, motstående genom hyp, du har hypen och vill dela upp i komposanter.
mg = Fx + Fy (komposanter i det lutande planet)
sin (23) = Fx/mg
cos(23) =Fy/mg
Är du med på att kraften kan beskrivas som mg sin (23)+0.17mg cos (23)?
Japp! Hur bör jag gå vidare med det?
Vad är sträckan som lådan ska förflyttas (Tips: använd trig)
0.5sin90/sin23 ?
Förklara hur du tänker
sinussatsen ger:
sin23/0.5=sin90/sträckan
Det fungerar absolut.
Du vet att w=f×s
Och att w=0.5mv^2
Kan du med hjälp av detta sätta upp en ekvation
-övningsprov-53.3.jpg?width=800&upscale=false) Efter sista "=" ska det stå 3.278.. vilket fortfarande är fel
Efter sista "=" ska det stå 3.278.. vilket fortfarande är fel
Där har du med felen vi pratade om tidigare
cos67=sin23, så det ändrade jag inte
sin23 har jag ändrat till cos23
Majskornet skrev:sinussatsen ger:
sin23/0.5=sin90/sträckan
Du söker alltså hyp, du har en katet. Definera hyp ex. som z nedan.
Vad var sin(23) igen, jo sin(23)=0,5/z
Lös ut z -> z= 0,5/sin(23)
cforsberg skrev:Majskornet skrev:sinussatsen ger:
sin23/0.5=sin90/sträckan
Du söker alltså hyp, du har en katet. Definera hyp ex. som z nedan.
Vad var sin(23) igen, jo sin(23)=0,5/z
Lös ut z -> z= 0,5/sin(23)
Varför söker jag hyp? Det är ju Fg som jag vet? Och i vilket led gör behöver jag göra det i min uträkning?
Majskornet skrev:cforsberg skrev:Majskornet skrev:sinussatsen ger:
sin23/0.5=sin90/sträckan
Du söker alltså hyp, du har en katet. Definera hyp ex. som z nedan.
Vad var sin(23) igen, jo sin(23)=0,5/z
Lös ut z -> z= 0,5/sin(23)
Varför söker jag hyp? Det är ju Fg som jag vet? Och i vilket led gör behöver jag göra det i min uträkning?
Det var sträckan som lådan ska transporteras. Då det kändes som du behöver bli lite mer säker på trigometrin. Jag behöver avvika nu, men ItzErre har detta i hamn tror jag - lycka till, till er båda! :)
cforsberg skrev:Majskornet skrev:cforsberg skrev:Majskornet skrev:sinussatsen ger:
sin23/0.5=sin90/sträckan
Du söker alltså hyp, du har en katet. Definera hyp ex. som z nedan.
Vad var sin(23) igen, jo sin(23)=0,5/z
Lös ut z -> z= 0,5/sin(23)
Varför söker jag hyp? Det är ju Fg som jag vet? Och i vilket led gör behöver jag göra det i min uträkning?
Det var sträckan som lådan ska transporteras. Då det kändes som du behöver bli lite mer säker på trigometrin. Jag behöver avvika nu, men ItzErre har detta i hamn tror jag - lycka till, till er båda! :)
Jaha, du menar så! Okej, tack för din hjälp hittills!
Är du med på
0.5mv^2=s(mg sin (23)+0.17mg cos (23))
Ta nu ett nytt blad och lös denna ekvationen
Tjoho! Det blev rätt! Jag hade glömt multiplicera med sträckan i min andra lösning, tack!
Men om jag får vara lite jobbig: går uppgiften att lösa genom rent energiresonemang som det jag försökt med här nedan?-övningsprov-53.jpg?width=800&upscale=false)
Ja, och nej.
Det är svårt att ta hänsyn till friktionskraften utan att använda f×s
Är det alltså ett nej, det är för krångligt?



-övningsprov-53.jpg?width=800&upscale=false)
-övningsprov-53.2.jpg?width=800&upscale=false)
