Enhetscirkeln

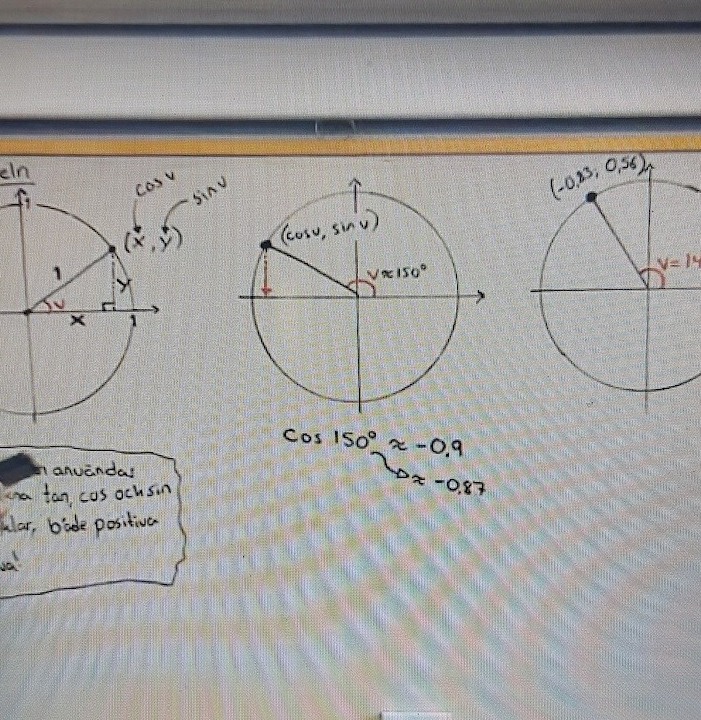
Om vinkeln är 0° eller 180° så är cisinusvärder 1.

Men vinkeln i videon verkar vara 150°.

Varför tycker du att cos(150°) bör vara lika med 1?

Oj jag ser nu att det är något jag missat men vet inte riktigt vad. (Jag missade genomgången om enhetscirkeln, videon är därför det första jag lär mig om den.)

OK. Jag rekommenderar starkt att du blir vän med enhetscirkeln. Lär dig hur den fungerar och hur du kan använda den.

Den insatsen kommer att betalas tillbaka mångdubbelt på prov och hemuppgifter.

Läs gärna detta avsnitt och fråga sedan oss om allt du vill att vi förklarar närmare.

Stort tack! Ska se det istället för videon. 

Det finns säkert massor med bra videos som förklarar enhetscirkeln på ett bra sätt.

Hoppas på att lyckas förstå den på egen hand, annars har jag en del att ta hand om. 😅

OK. Men annars frågar du oss, eller hur?

Här kommer en fråga! Jag förstår inte vad som gör att det som visas i bilderna stämmer. Vad är resonemangen?

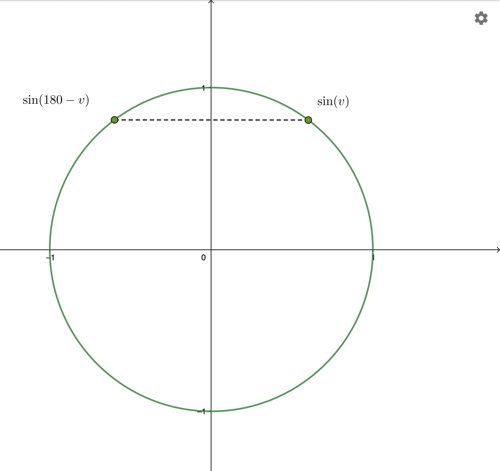
Om första bilden: Varför är det sin(180-v) i punkten till vänster och inte bara sin(v)?

Bra fråga.

På grund av symmetri så är den blåmarkerade vinkeln v till höger lika stor som den blåmarkerade vinkeln till vänster.

Eftersom ett halvt varv är 180° så är den rödmarkerade vinkeln 180°-v.

Sinusvärdet för en vinkel är lika med den vertikala koordinaten för skärningspunkten mellan radien och cirkeln.

Den horisontella streckade linjen indikerar att de vertikala koordinaterna för punkt A och punkt B är lika stora.

Alltså är sin(v) = sin(180°-v)

Blev det tydligare då?

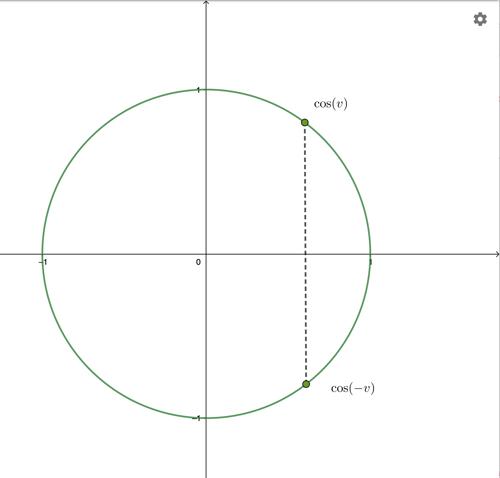
Ja! Andra bilden förstår jag dock fortfarande inte. Hur resonerar jag där? 

Ett utmärkt tillfälle för dig att pröva ett liknande resonemang på andra bilden.

Rita en radie till respektive punkt på enhetscirkeln, markera vinkeln v mot den övre radien.

Fundera på

• Vad är vinkeln mot den undre radien (tänk symmetri).
• Vad innebär den vertikala streckade linjen mellan de två punkterna?
• Hur hänger cosinusvärdet v av en vinkel ihop med koordinaterna för en punkt på enhetscirkeln?

Gjorde allt du sa men kom inte fram till så mycket. Cosinusvärdet v av en vinkel visar x-koordinaten för den punkten på cirkelns rand. Den vertikala streckade linjen mellan de två punkterna visar att punkterna är symmetriska kring x-axeln. Längre än så kommer jag inte. 

Dessutom undrar jag: Gäller samma resonemang för både sinus och cosinus i de två bilderna? Alltså, om vi bytte ut sin mot cos i den första bilden – skulle det fortfarande stämma? Och om vi bytte ut cos mot sin i den andra bilden – fungerar resonemanget då också?

Dr.scofield skrev:

Gjorde allt du sa men kom inte fram till så mycket. Cosinusvärdet v av en vinkel visar x-koordinaten för den punkten på cirkelns rand. Den vertikala streckade linjen mellan de två punkterna visar att punkterna är symmetriska kring x-axeln. Längre än så kommer jag inte. 

Det stämmer.

Eftersom punkterna har samma horisontella koordinat så representerar de även samma cosinusvärde.

Symmetrin ger även att vinkeln ner till den undre radien är -v.

Allt detta tillsammans visar att cos(v) = cos(-v).

Dessutom undrar jag: Gäller samma resonemang för både sinus och cosinus i de två bilderna? Alltså, om vi bytte ut sin mot cos i den första bilden – skulle det fortfarande stämma? Och om vi bytte ut cos mot sin i den andra bilden – fungerar resonemanget då också?

Nej då funkar det inte.

• Sinusvärdet är den vertikala koordinaten
• Cosinusvärdet är den horisontella koordinaten

Du ser att de två punkterna i den övre bilden har samma vertikala koordinater men olika horisontella koordinater.

Du ser att de två punkterna i den undre bilden har samma horisontella koordinater men olika vertikala koordinater.

Hänger med! Tack för hjälpen! :) 

Vad bra!

Bli kompis med enhetscirkeln!