Enhetscirkeln
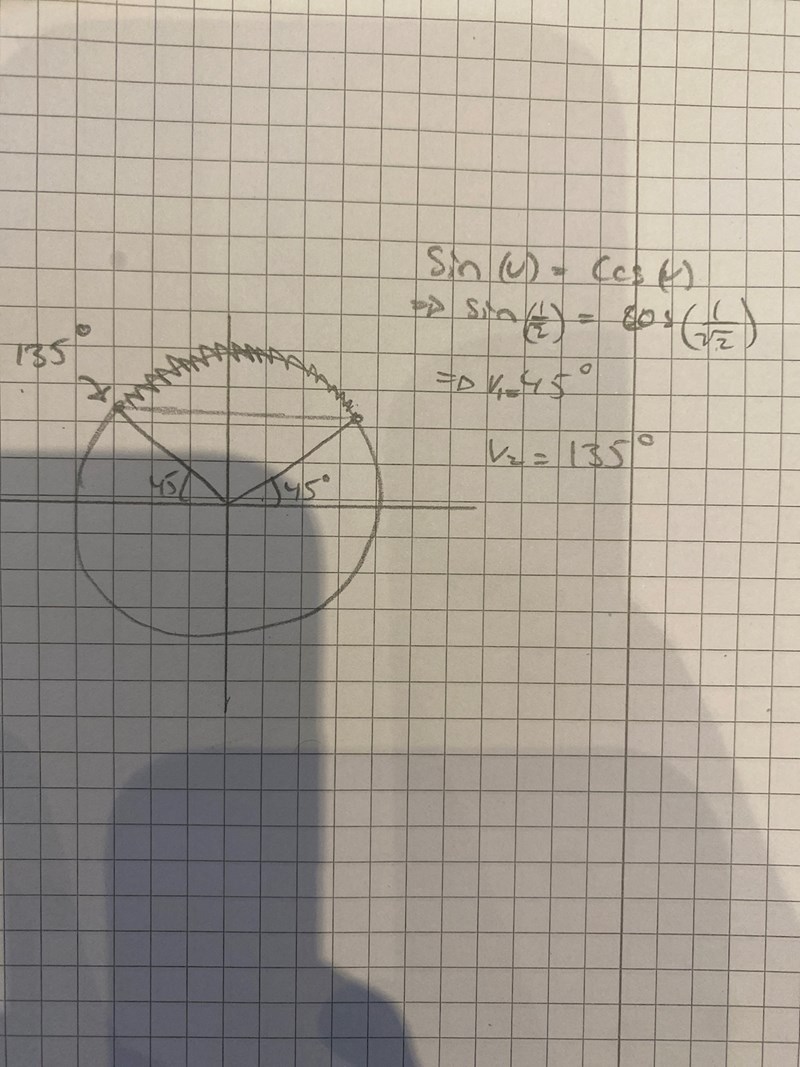
Hur ska jag tänka när jag löser denna uppgift. Jag ritar upp enhetscirkeln och förstår att intervallet börjar från 45 grader men när slutar det då?

Olikheten sin v ≥ cos v betyder ju att y-koordinaten av punkten på enhetscirkeln är större än punktens x-koordinat.
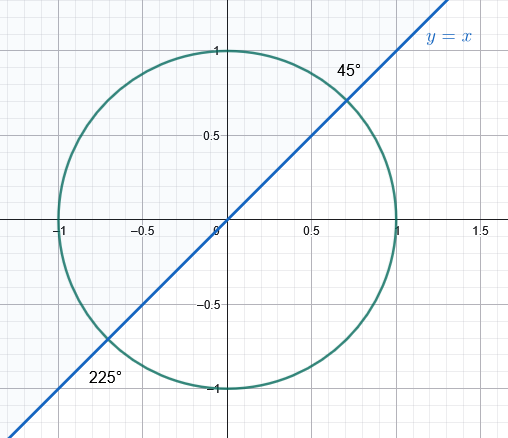
Kan du rita enhetscirkeln och linjen y=x i samma koordinatsystem?
För vilka vinklar på enhetscirkeln är y ≥ x?
Är det över linjen y=x, eller under den?
LuMa07 skrev:Olikheten sin v ≥ cos v betyder ju att y-koordinaten av punkten på enhetscirkeln är större än punktens x-koordinat.
Kan du rita enhetscirkeln och linjen y=x i samma koordinatsystem?
För vilka vinklar på enhetscirkeln är y ≥ x?
Är det över linjen y=x, eller under den?
det är väll över?
Exakt, det är punkter över linjen y=x.
Vilka vinklar blir det, då?
LuMa07 skrev:Exakt, det är punkter över linjen y=x.
Vilka vinklar blir det, då?
jag tänker att det blir från 45 till 135 grader, men det står inte så i facit. Det står från 45 till 225 grader, förstå liksom inte varför
Kan du visa upp din figur där du ritat enhetscirkeln och linjen y=x?
Var är linjen y=x i din figur?
LuMa07 skrev:Var är linjen y=x i din figur?
Jag rita den mellan punkterna
Nej, det har du inte gjort. Du har ritat ut:
- en sträcka med lutning -1 till vänster om y-axeln, d.v.s. en del av linjen y=-x,
- en sträcka med lutning +1 till höger om y-axeln, d.v.s. en del av linjen y=x.
Du borde ha ritat linjen y=x både till vänster och till höger om y-axeln.
LuMa07 skrev:Nej, det har du inte gjort. Du har ritat ut:
- en sträcka med lutning -1 till vänster om y-axeln, d.v.s. en del av linjen y=-x,
- en sträcka med lutning +1 till höger om y-axeln, d.v.s. en del av linjen y=x.
Du borde ha ritat linjen y=x både till vänster och till höger om y-axeln.
Skulle du kunna visa hur
LuMa07 skrev:
ska jag alltid tänka att jag drar ett rakt streck från min ursprungsvinkel då till andra sidan?
Man ska utgå från frågeställningen. Det var givet i uppgiften att du ska lösa olikheten sin v ≥ cos v, d.v.s. y ≥ x. Då kan man rita den räta linjen y=x för att hitta gränserna.
LuMa07 skrev:Man ska utgå från frågeställningen. Det var givet i uppgiften att du ska lösa olikheten sin v ≥ cos v, d.v.s. y ≥ x. Då kan man rita den räta linjen y=x för att hitta gränserna.
jahaa nu förstår jag var du menar med y=x, trodde du menade sinv= cosv först