Enhetscirkeln - exakta värden

Tänk dig enhetscirkeln. Du vet att sin (v) = sin (v + n× 360)

Dvs 600 = v + n × 360. Om n=1 vad blir v ? I vilken kvadrant av enhetscirkeln befinner vi oss då? 

Du vet antagligen också att sin (v) = sin ((180 - v) + n × 360). Om n = 1, vad blir v? I vilken kvadrant befinner vi oss då. Övertyga dig om att sinus blir detsamma. 

ostertalje skrev:

Tänk dig enhetscirkeln. Du vet att sin (v) = sin (v + n× 360)

Dvs 600 = v + n × 360. Om n=1 vad blir v ? I vilken kvadrant av enhetscirkeln befinner vi oss då? 

Du vet antagligen också att sin (v) = sin ((180 - v) + n × 360). Om n = 1, vad blir v? I vilken kvadrant befinner vi oss då. Övertyga dig om att sinus blir detsamma. 

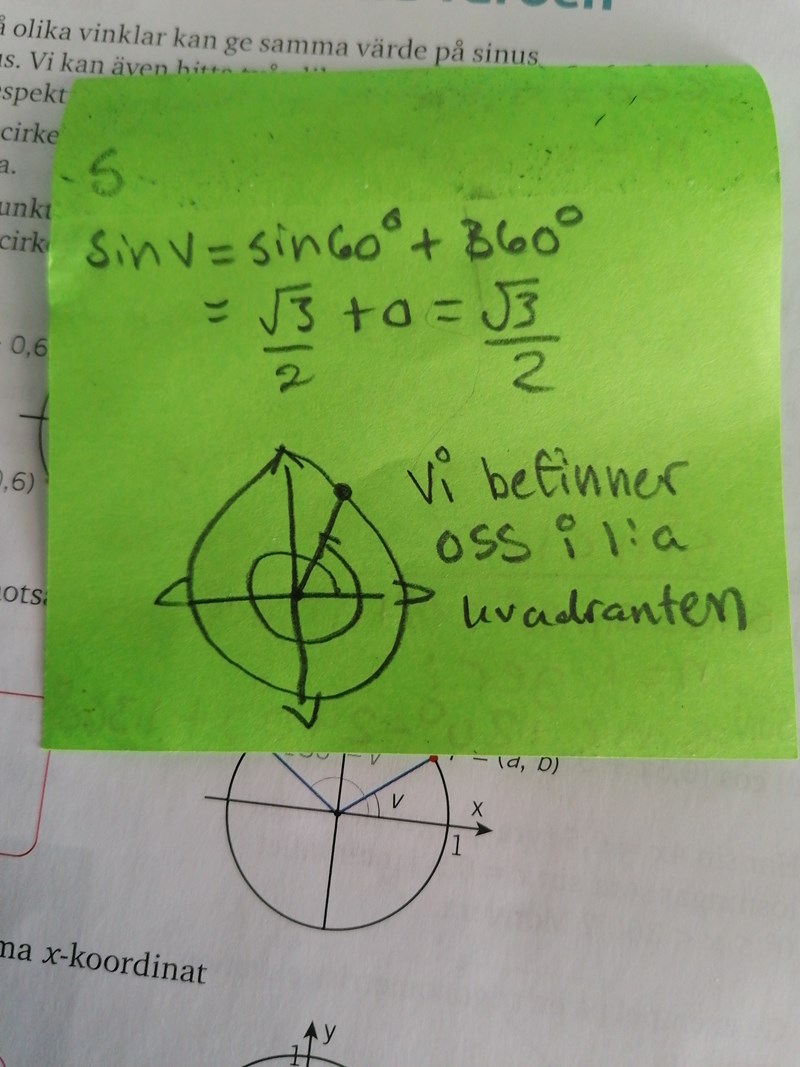
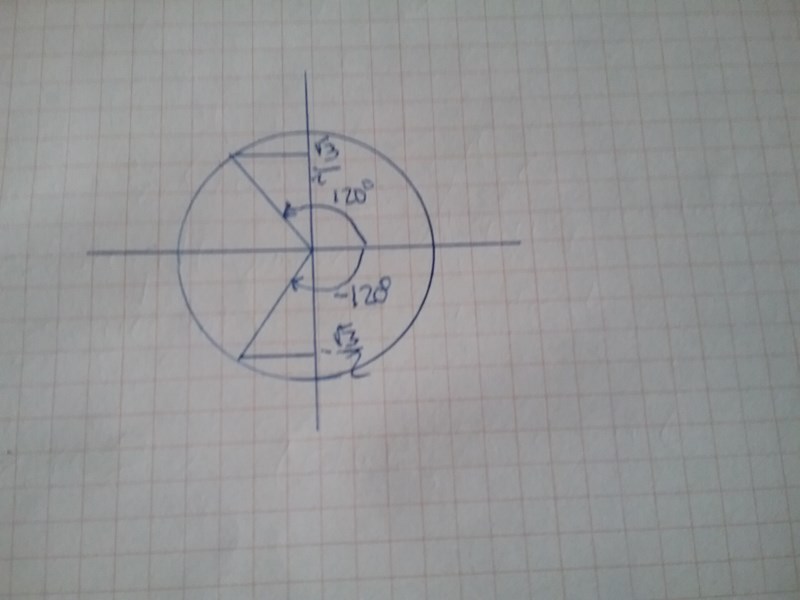
Jag tror jag förstår vad du menar, men ändå inte. Jag får v till 240° och vi befinner oss i den 3:e kvadraten. Därefter får jag $\sin v=\frac{\sqrt{3}}{2}$ vilket är ett inkorrekt svar.  I det befinner vi oss i den första kvadranten.

180-240+360 = 300.

Du drar ju en korrekt slutsats på den första lappen, vinkeln är 240 och det blir i 3:e kvadranten.  Men vad har sin för tecken i 3:e kvadranten? Fyll i tabellen i uppg 1155 så förstår du.

ostertalje skrev:

Du drar ju en korrekt slutsats på den första lappen, vinkeln är 240 och det blir i 3:e kvadranten.  Men vad har sin för tecken i 3:e kvadranten? Fyll i tabellen i uppg 1155 så förstår du.

Okej. Jag drar den slutsats att $\sin 120°$har ett positivt värde på $\frac{\sqrt{3}}{2}$.

Eftersom jag vet detta vet jag då att $\sin (-120°)$har ett negativt värde på $\frac{\sqrt{3}}{2}$.

Dessutom tror jag att jag skulle med mer kunskap kunna veta att $\sin (-120°)$befinner i den tredje kvadranten. 

Det kan finnas fler lösningar till denna antar jag.

Bra. Eftersom 600 grader är 360 + 240 så är det vinkeln 240 som vi söker. Du har också förstått att +240 och -120 är samma vinkel. Dessutom vet man att om sin(120)= roten ur 3 dividerat med 2 så är sin(-120)=-roten ur 3 dividerat med 2.

Några andra andra lösningar kan det inte bli. Sin(600) är en bestämd vinkel och den vinkeln kan bara ha ett sinus-värde.