Enhetsnormalen för Y1

Här är resten av exemplet

Man måste inte parametrisera $Y_1$ för att se att en enhetsnormal till ytan $Y_1$ är $(0,0,1)$ eftersom normalen ska peka rakt upp i $\hat{z}$-led.

Integralen kan sedan beräknas trivialt eftersom vi vet att ytan av en cirkel är $\pi r^2$.

Men en parameterframställning av cirkelytan $Y_1$ kan t.ex. vara

$\,\,Y_1:\quad \mathbf{r}=\mathbf{r}(r,\theta)=(r\cos(\theta), r\sin(\theta), 0),\quad (r,\theta)\in D$

Det vektoriella ytelementet med rätt normering för vår parameterframställning blir då

$\displaystyle \,\,\mathrm{d}\mathbf{S}=\frac{\partial \mathbf{r}}{\partial r}\times \frac{\partial \mathbf{r}}{\partial \theta}\,\mathrm{d}r\mathrm{d}\theta=(0,0,r)\,\mathrm{d}r\mathrm{d}\theta$

$\displaystyle \,\,\iint_{Y_1}\mathbf{u}\cdot \mathrm{d}\mathbf{S}=\int_0^{2\pi}\int_0^{2}\,(r\cos(\theta), r\sin(\theta), 3)\cdot (0,0,r)\mathrm{d}r\mathrm{d}\theta=12\pi$

Tack så mycket det var till stor hjälp 

Hej, igen 

så om till exempel cirkelen har radie 2, så blir normalen lik (0,0,2)

Det vektoriella ytelementet

$\mathrm{d}\mathbf{S}=\frac{\partial \mathbf{r}}{\partial r}\times \frac{\partial \mathbf{r}}{\partial \theta}\,\mathrm{d}r\mathrm{d}\theta$

är det riktat utmed normalen, med längden lika med arean av den parallellogram som spänns av de två vektorerna $\frac{\partial \mathbf{r}}{\partial r},\, \frac{\partial \mathbf{r}}{\partial \theta}$

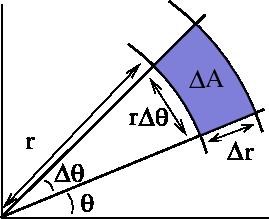Det innebär att normalen $(0,0,r)$ har olika storlek på olika delar av ytan.

Om du istället använder rektangulära koordinater $(x,y)$ är enhetsnormalen $(0,0,1)$ så länge ytan är plan. Normalen är då $(0,0,1)$.

Du bestämmer själv om du vill räkna med en enhetsnormal (och konvertera till polära koordinater senare) eller om du vill göra en parameterframställning och låta normeringen följa med på köpet.

Men det är viktigt att du ser till att ytnormalen har rätt längd (normering )och rätt riktning. Annars får naturligtvis integralen fel värde.

En annan vanlig normering är när du har en parameterframställning $\mathbf{r}(x,y)=(x,y,z(x,y))$ över ett område i xy-planet.

Då blir

$\mathbf{r}^{'}_x\times\mathbf{r}^{'}_y=(-z^{'}_x,-z^{'}_y,1)$

Då  $z(x,y)=0$ blir $\mathbf{r}(x,y)=(x,y,0)$ och

$\frac{\partial \mathbf{r}}{\partial x}\times \frac{\partial \mathbf{r}}{\partial y}=(0,0,1)$

Tack så mycket det var till stor hjälp 

mvh

suad