Enkel teorifråga om rader i matriser och surjektivitet
Tjena pluggakuten!
Har en fråga om uppgift c)
 Facit:
Facit:
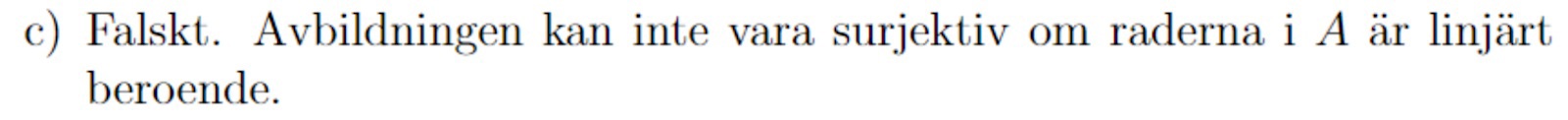
Hur kan de koppla om raderna i A är linjärt beroande till ifall de är surjektiva eller inte, och hur påverkar surjektivitetrn hurvida ekvationen har en lösning för varje b?
Tacksam för svar!
Etthejfrånpolhem skrev:[...] hur påverkar surjektivitetrn hurvida ekvationen har en lösning för varje b?
Det följer av definitionen av surjektivitet! Avbildningen som mappar är surjektiv om och bara om den träffar varje vektor i , dvs. om det för varje i målmängden finns en vektor i definitionsmängden, sådan att .
Mer genrellt så är mängden av alla vektorer in som avbildningen träffar, och mängden av alla för vilka ekvationen har en lösning båda lika med columnrummet .
Hur kan de koppla om raderna i A är linjärt beroande till ifall de är surjektiva eller inte [...]?
Det finns många olika sätt att tänka på detta! Så här tänker jag personligen (andra får gärna fylla på med sina favoritargument!):
Om raderna i är linjärt beroende så betyder det att det finns en icke-trivial linjärkombination av dem som ger 0, dvs. det finns någon vektor sådan att
där jag med menar den :te radvektorn av .
Speciellt gäller detta kolumnvis, dvs. för den :te kolumnvektorn så har vi
Alltså har vi upptäckt att alla kolumnerna i uppfyller en ekvation: de är vektorer sådana att
Geometriskt kan man se det som att alla kolumnvektorerna är instängda i ett och samma hyperplan i , med dimensionen .
Eftersom alla kolumnerna uppfyller den här ekvationen kommer även alla linjärkombinationer av kolumnerna också att uppfylla ekvationen (varför?).
Ett ekvivalent sätt att formulera detta är att säga att den linjära avbildningen kommer bara att träffa vektorer som uppfyller den här ekvationen. Dvs. vi kommer missa nästan alla vektorer i , så den linjära avbildningen är långt ifrån surjektiv!
Här kommer ett lite mer abstrakt sätt att formulera beviset på:
- Att raderna i är linjärt beroende betyder att det finns en nollskild vektor .
- Vi har att (varför?).
- Alltså har är .
- Det betyder att .
- Eftersom är precis bilden av den linjära avbildningen, dvs. mängden av alla vektorer som träffar, så betyder detta är avbildningen inte är surjektiv.
Man kan också tänka i termer av rang:
- En av de viktigaste satserna i linjär algebra är att dimensionen av radrummet hos en matris altid är lika med dimensionen av kolumnrummet, dvs. dim(row(A))=dim(col(A)). Detta tal brukar man kalla rangen av A, och skriva som rank(A).
- Om vi nu vet att raderna i A är linjärt beroende så betyder det att dim(row(A))<m, dvs. rank(A)<m.
- Men det betyder alltså att dim(col(A))<m, dvs. col(A) är ett underrum av längre dimension av .
- Eftersom col(A) är precis mängden av alla vektorer som den linjära avbildningen träffar, så betyder detta är avbildningen inte är surjektiv.
Tack så mycket för svaren Oggih! Väldigt bra förklarat, nu hänger jag med!


