Envariabel - differentialekvation
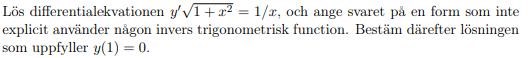
Suttit fast på uppgiften ovan ett tag nu och hade uppskattat lite hjälp för att komma igång/få till något svar.
Tack på förhand.
Du har förmodligen fått integralen .
Edit: Har du provat variabelbytet ?
Edit: Såg precis att jag löst en annan uppgift än den du specificerade. Det saknas ett x^2 innanför roten i mitt inlägg. Du kan bortse från mitt förslag.
Hej. Jag har ett förslag.
Med informationen ovan kan integralen omvandlas till
När man väl kommit hit måste man dela upp i partialbråk. Vet du hur man gör det?
Senaste inlägg är felaktigt.

@dr_lund
Har provat med variabelbytet men inte helt säker om detta bryter mot uppgiftens anvisningar att man ej ska använda någon invers trigonometrisk funktion? Tackar i vilket fall som helst.
@oneplusone2
Jo det är väl att man sätter in konstanter i uttrycket så att och sedan löser ekvationssystemet som ges av denna för att bestämma A och B har jag för mig. Kan prova med det och återkomma. Tack för förslaget!
Edit: Ah, såg misstaget i ditt förslag, testar igen med dr_lunds förslag :)
Inte så enkel integral.
Jag hjälper dig en bit på vägen.
. Den första termen är enkel. Fundera ett tag på .
I slutändan, efter fullgjord integrering, byter du tillbaka till cartesiska koordinater.
Inga trigonometriska substitutioner är nödvändiga...
AlvinB skrev:Inga trigonometriska substitutioner är nödvändiga...
Har du gjort uppgiften fullt ut med den substitutionen?
osv
Tackar för alla svar! Har prövat med trigonometriska substitutioner och identiteter men körde fast efter ett tag. Det funkade lite bättre med @AlvinB förslag, fick till slut svaret . Orkar inte skriva ner hela uträkningen här men @Kallaskull har ju skrivit ner en del i alla fall. Dock inte säker om jag har gjort rätt.
Kan även fylla i lite på dr_lunds lösning med tangens-substitutionen. Den går till så här:
Det här är en sådan där standardintegral som är ganska krånglig, men det finns några fultrick för att göra den snabbt. Hade man aldrig sett den förut hade man nog kört på en sådan där -substitution, men för den mer erfarne finns ett enklare sätt:
, ger nu:
vilket är nästan samma svar som Matteosv fick (Det är jätteviktigt att ta med absolutbeloppen!).
Bra och utförligt, AlvinB. Jag gjorde mig skyldig till ett fel i mitt tidigare svar;

Det ska förstås vara
osv. enligt AlvinB. Rätt ska vara rätt!