Envariabelanalys - Visa att funktion är konkav

Hej! Jag skulle behöva hjälp med den här uppgiften.

Min tankegång hittills är att jag kan använda mig av definitionen för en konkav funktion, som lyder:

En funktion $f$ sägs vara konkav i $[a, b] \subseteq D_{f}$ om $- f$ är konvex i $[a, b]$ .

Jag tänker då att om jag lyckas visa att $- f$ är konvex i intervallet då har jag väl visat att $f$ är konkav i intervallet?

Hur jag kan komma fram till detta med hjälp av given information har jag ingen aning om.

Om f är avtagande ---> f'<0

Om f' är avtagande ----> f''<0 vilket betyder att f är konkav.

Mohammad Abdalla skrev:
Om f är avtagande ---> f'<0

Om f' är avtagande ----> f''<0 vilket betyder att f är konkav.

Jag håller med om att detta stämmer, men skulle detta verkligen vara tillräckligt som ett svar? Är det inte alltid så att man ska utgå ifrån definitionen och visa att påståendet stämmer överens med den?

Med tanke på hur du definierat konkav - hur definieras konvex?

Smaragdalena skrev:
Med tanke på hur du definierat konkav - hur definieras konvex?

Definition: Funktionen $f$ är konvex i ett intervall $[a, b] \subset D_{f}$ om det för varje $x_{1}, x_{2} \in [a, b]$ gäller att

$f (t x_{1} + (1 - t) x_{2}) \leq t f (x_{1}) + (1 - t) f (x_{2})$ för alla $0 \leq t \leq 1$

Kan du berätta med ord vad detta betyder?

Smaragdalena skrev:
Kan du berätta med ord vad detta betyder?

Det innebär som jag tolkar det: Att om vi har två valfria punkter på funktionsgrafen i intervallet och drar en sekant mellan dessa så kommer varje punkt på sekanten alltid ha ett funktionsvärde större än eller lika med funktionsvärdet som den ursprungliga funktionen antar i samma punkt.

Edit: Alltså kommer sekanten alltid att ligga ovanför eller längs med funktionsgrafen om det är en konvex funktion.

Kan du rita (på valfritt sätt) ett exempel på en konvex kurva och lägga upp bilden här?

Det verkar somom det är en konkav kurva du definierar i ord.

Smaragdalena skrev:
Kan du rita (på valfritt sätt) ett exempel på en konvex kurva och lägga upp bilden här?

Det verkar somom det är en konkav kurva du definierar i ord.

T.ex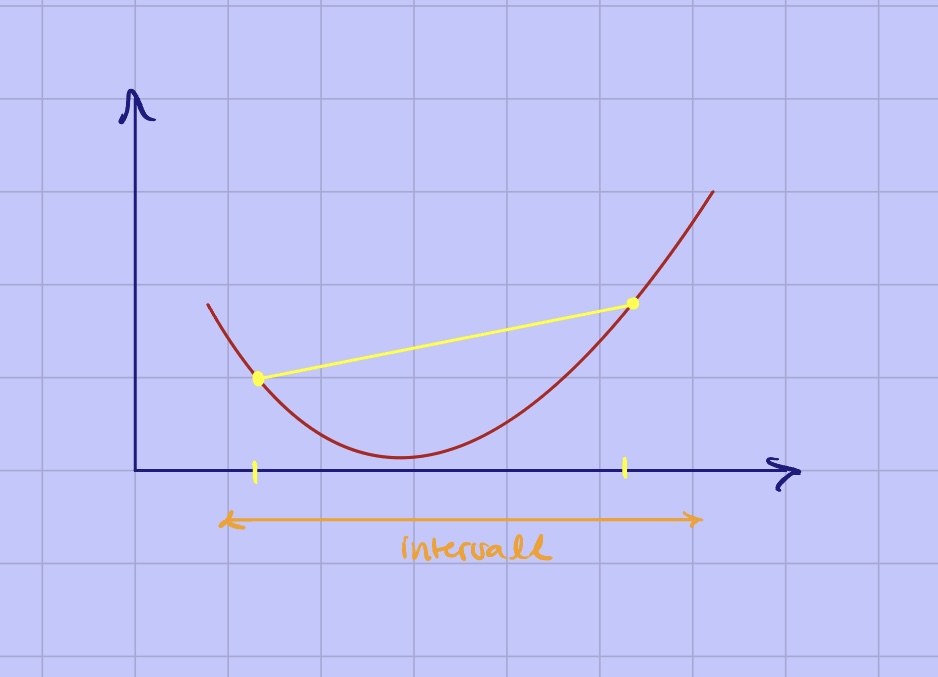

Smaragdalena skrev:
Kan du rita (på valfritt sätt) ett exempel på en konvex kurva och lägga upp bilden här?

Det verkar somom det är en konkav kurva du definierar i ord.

https://en.wikipedia.org/wiki/Convex_function

Om du skrollar ner lite till definitionen.

https://en.wikipedia.org/wiki/Concave_function

@Luffy, det finns också exempel om du skrollar ner lite, kan detta gör livet enklare för dig eller är det fortfarande oklart?

Dracaena skrev:
@Luffy, det finns också exempel om du skrollar ner lite, kan detta gör livet enklare för dig eller är det fortfarande oklart?

Det jag inte riktigt förstår är hur man ska sammankoppla att $f'$ är avtagande till definitionen för en konkav funktion.

Jag antar att man på något sätt måste bevisa att detta stämmer överens med definitionen för att fullständigt bevisa att det gäller. Annars som Mohammad Abdalla skrev i #2 "så Om f' är avtagande ----> f''<0 vilket betyder att f är konkav.", vilket i sig stämmer för att det verkar logiskt och ser logiskt ut om man ritar upp det, men även detta har ju inte bevisats.

Jag kanske övertänker och det kanske är för komplicerat för att visa det sättet jag tänker, men det känns helt enkelt "för simpelt" att endast säga att andraderivatan är negativ och därför är funktionen konkav och det är väl inte heller något "bevis".

Bump

Försök bevisa

Om andraderivatan är negativ, så är förstaderuvatan avtagande
Om förstaderivatan är avtagande, så är funktionen konvex

Om du behöver hjälp med detta, så skriv här i tråden.

Svara

Visa senaste svar