Envariabelkalkyl - gränsvärde

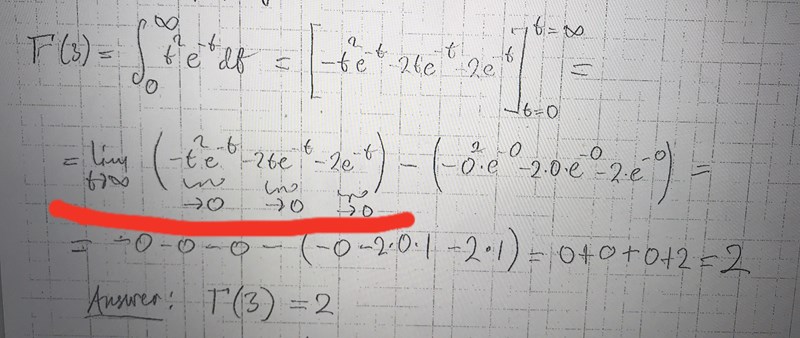
Det är ett standardgränsvärde, se:

http://www2.math.uu.se/~asplund/repenvar/stdgrv.pdf

Man kan också härleda det genom att tillämpa l’Hôpitals regel upprepade gånger.

$\frac{d^{n+1}}{dx^{n+1}}x^n=0$

$\frac{d^{n+1}}{dx^{n+1}}e^x=e^x$

Exponentialfunktionen går mot oändligheten snabbare än varje polynom. Man kan visa det t.ex. med l'Hopitals regel.

Hur är det man ska se det som ett standardgränsvärde? Är det x^a/b^x = 0 när x går mot oändligheten från länken du skickade som man ska använda då? I mitt fall, blir det då -t^2/(1/e^t)-2t/(1/e^t)-2/(1/e^t) = 0 där 1/e^t = b^x? Eller hur ska man tänka?

$\frac{t^2}{e^t}=\frac{t^a}{b^t}$ då $a=2,b=e>1$.

Tack då förstår jag!