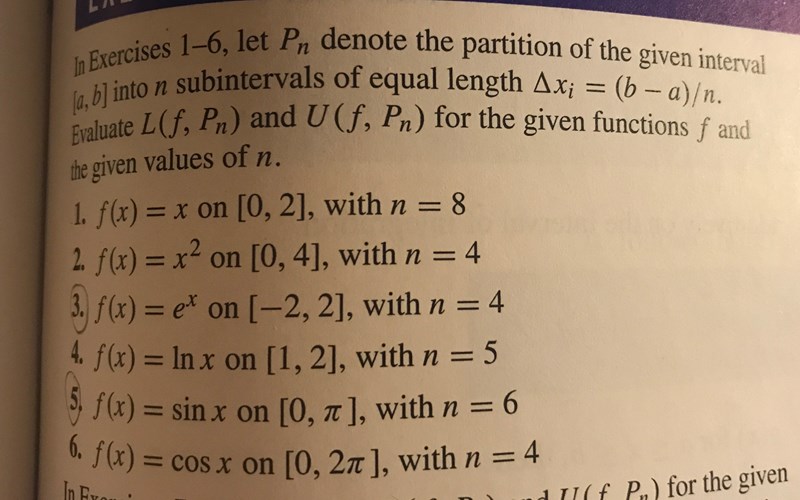Envariabelkalkyl - Riemannsumma

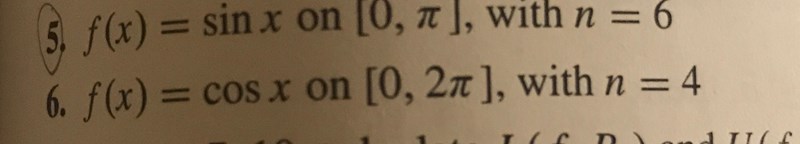
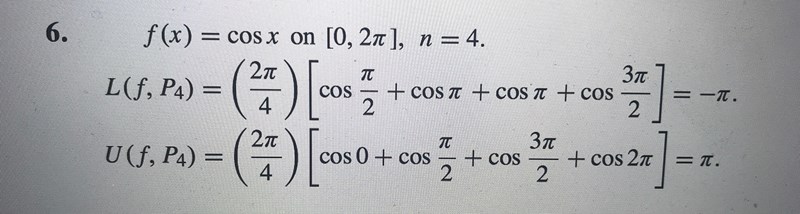
Vad är frågan? Hur är den formulerad?

Vad betyder L respektive U i din bok? Är det upper respektive lower?

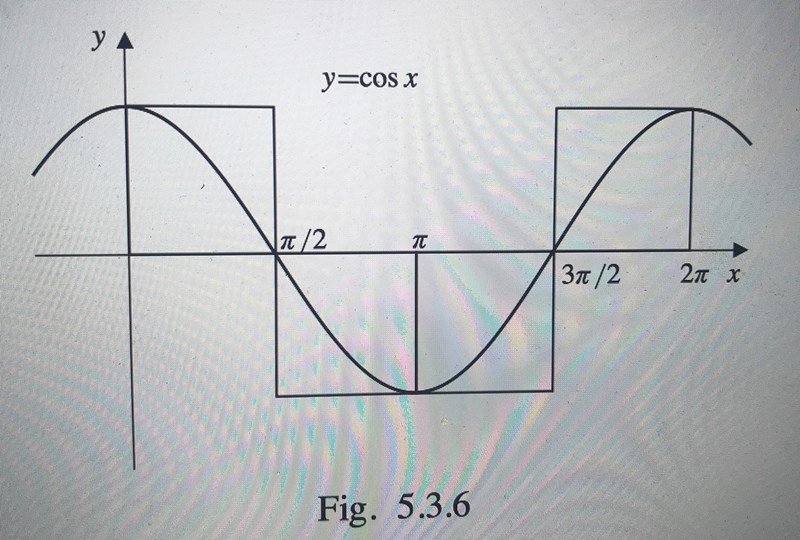
Översumman har y-värdena 1 0 0 respektive 1 i de fyra intervallen. Undersumman har y-värdena 0 -1 -1 0 i de fyra intervallen.

Ja precis. Jag förstår inte varför det blir cos(pi/2+cos(pi/2) på översumman?

Bilden är för både översumman och undersumman. Summorna är definierade som:

$$\begin{gathered} P_N=(a=x_0, x_1, ..., x_N=b) \\ U(f, P_N)=\frac{b-a}{N}\sum _{i=1}^{N}f(x_i*) \mathrm{där} f\left(x\right)\le f(x_i*) \\ L(f, P_N)=\frac{b-a}{N}\sum _{i=1}^{N}f(x_i*) \mathrm{där} f\left(x\right)\ge f(x_i*) \end{gathered}$$

Med andra ord är de två rektanglarna ovanför x-axeln översumman och de under x-axeln undersumman. Du kan leka med denna applet för att öka förståelsen: Upper and lower Riemann sum

Jag har bara gjort uppgifter där grafen är över x-axeln, hur ska man tänka när den är under x-axeln som i den här uppgiften?

Hej!

Uppgift 6. 

Steg 1. Intervallet $[0,2\pi]$ delas in i $n=4$ stycken delintervall

    $\displaystyle [0,2\pi] = [t_0,t_1)\cup [t_1,t_2)\cup[t_2,t_3)\cup[t_3,t_4]$

där $t_0=0$ och $t_4=2\pi$ och övriga ändpunkter ges av $t_k = \frac{k}{4}\cdot 2\pi.$

Steg 2. Integralen $\int\limits_{0}^{2\pi}f(x)\,dx$ skrivs som en summa av integraler över delintervall.

    $\displaystyle\int\limits_{0}^{2\pi} = \int\limits_{t_0}^{t_1} +\int\limits_{t_1}^{t_2}+\int\limits_{t_2}^{t_3}+\int\limits_{t_3}^{t_4}.$

Steg 3. Över intervallet $[t_0,t_1)$ ersätts den varierande funktionen $f(x)$ med den konstanta funktionen $f(t_0)$; det betyder att integralen $\int\limits_{t_0}^{t_1}f(x)\,dx$ ersätts med talet $\int\limits_{t_0}^{t_1}f(t_0)\,dx = f(t_0)\cdot (t_1-t_0)$. Detta medför att integralen $\int\limits_{0}^{2\pi}f(x)\,dx$ ersätts med den undre summan

    $L(f,P_4) = f(t_0)(t_1-t_0)+f(t_1)(t_2-t_1)+f(t_2)(t_3-t_2)+f(t_3)(t_4-t_3).$

Steg 4. Över intervallet $[t_0,t_1)$ ersätts den varierande funktionen $f(x)$ med den konstanta funktionen $f(t_1)$; det betyder att integralen $\int\limits_{t_0}^{t_1}f(x)\,dx$ ersätts med talet $\int\limits_{t_0}^{t_1}f(t_1)\,dx = f(t_1)(t_1-t_0).$ Detta medför att integralen $\int\limits_{0}^{2\pi}f(x)\,dx$ ersätts med den övre summan

    $U(f,P_4)=f(t_1)(t_1-t_0)+f(t_2)(t_2-t_1)+f(t_3)(t_3-t_2)+f(t_4)(t_4-t_3).$

Steg 5. Med funktionen $f(x)=\cos x$ och $t_k = \frac{k}{4}\cdot 2\pi$ blir den undre summan 

    $\displaystyle L(f,P_4)=\frac{\pi}{2}\cdot \{\cos 0 + \cos\frac{\pi}{2} + \cos\pi + \cos\frac{3\pi}{2}\}=\ldots$

och den övre summan

    $\displaystyle U(f,P_4)=\frac{\pi}{2}\cdot\{\cos \frac{\pi}{2}+\cos\pi+\cos\frac{3\pi}{2} + \cos 2\pi\}=\ldots .$