Envariabelkalkyl - volym av kropp

Jag förstår till att börja med inte vad det står på första raden.

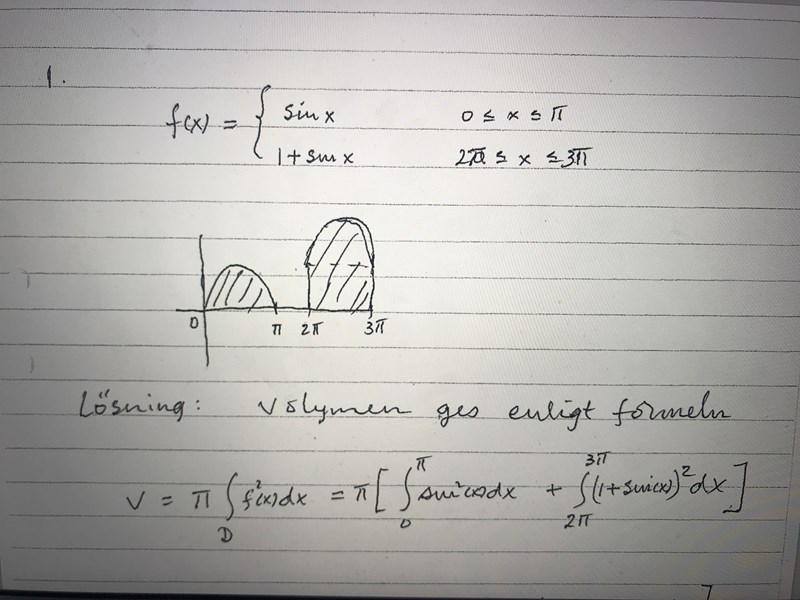
Det här är början på lösningen

Det där ser ut som en helt annan uppgift! (Det verkar vara facit till uppgift 1, men vi är på uppgift 3?)

Till den här uppgiften skall du väl ändå beräkna integralen:

$\displaystyle\pi\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\left(3\sin\left(x\right)\right)^2\ dx$

Oj jag råkade skicka fel fråga, nu har jag ändrat

Facit har ett fulknep (ett väldigt omständigt sådant) för att beräkna integralen:

$\displaystyle\int_0^\pi\sin^2\left(x\right)\ dx$

Vad man gör är att man tillämpar partialintegration:

$\displaystyle\int_a^b f\left(x\right)g\left(x\right)\ dx=[f\left(x\right)G\left(x\right)]_a^b-\int_a^bf'\left(x\right)G\left(x\right)\ dx$

och låter $f(x)=\sin(x)$ och $g(x)=\sin(x)$. Då blir $f'(x)=\cos(x)$ och $G(x)=-\cos(x)$. Partialintegrationsformeln ger då:

$\displaystyle\int_0^\pi\sin^2\left(x\right)\ dx=\int_0^\pi\sin\left(x\right)\cdot\sin\left(x\right)\ dx=\underbrace{[\sin\left(x\right)\cdot\left(-\cos\left(x\right)\right)]_0^\pi}_{=0}-\int_0^\pi-\cos\left(x\right)\ dx=$

$=\displaystyle\int_0^\pi\cos^2\left(x\right)\ dx$

Vi får alltså likheten:

$\displaystyle\int_0^\pi\sin^2\left(x\right)\ dx=\int_0^\pi\cos^2\left(x\right)\ dx$

Med trigonometriska ettan får vi sedan att $\cos^2(x)=1-\sin^2(x)$:

$\displaystyle\int_0^\pi\sin^2\left(x\right)\ dx=\int_0^\pi1-\sin^2\left(x\right)\ dx$

$\displaystyle\int_0^\pi\sin^2\left(x\right)\ dx=\int_0^\pi1\ dx-\int_0^\pi\sin^2\left(x\right)\ dx$

$\displaystyle\int_0^\pi\sin^2\left(x\right)\ dx=\pi-\int_0^\pi\sin^2\left(x\right)\ dx$

Om vi nu adderar integralen till båda led får vi:

$\displaystyle\int_0^\pi\sin^2\left(x\right)\ dx+\int_0^\pi\sin^2\left(x\right)\ dx=\pi-\cancel{\int_0^\pi\sin^2\left(x\right)\ dx+\int_0^\pi\sin^2\left(x\right)\ dx}$

$\displaystyle2\int_0^\pi\sin^2\left(x\right)\ dx=\pi$

$\displaystyle\int_0^\pi\sin^2\left(x\right)\ dx=\frac{\pi}{2}$

Och vips så har vi trollat fram att integralens värde är $\pi/2$!

Detta tycker jag är väldigt krångligt. Det går även att få fram värdet med hjälp av identiteten:

$\sin^2\left(x\right)=\dfrac{1-\cos(2x)}{2}$

vilket är betydligt vanligare än att göra allt det där krånglet med partialintegration.

Åhh tack så jättemycket för hjälpen!!