Envarre med slag av fourier

Säg att vi har en funktionsföljd g_n—>g på alla kompakta delmgdr av (a,b]. Kan vi därav dra slutsatsen att den konvergerar på hela (a,b]? Nej, konvergensen här innebär att vi till varje epsilon kan finna ett N sådant att |g_n-g|<=epsilon för n>N. Men när x närmar sig t ex a så kan vi behöva ta allt större N för att olikheten ska gälla. Konvergensen på kompakta delmängder innebär bara att vi kan hitta ett N över huvud taget så länge vi håller oss på visst avstånd från a,inte hur stort detta N måste vara. Därför kan du inte ersätta [delta,pi] med (0,pi].

Hur kan han då efter tavlan längst ner dra slutsatsen att den är likformigt konvergent på (0,pi)?

På bilden, alldeles ovan för hjässan med blonda håret står hans slutsats: konvergerar likformigt på halvöppna intervallet delta<=x< pi, vilket är korrekt. Alltså inte det öppna intervallet (0,pi). Notera att likformig konv på kompakta delmängder av en mängd A medför punktvis konv på hela A. Detta följer helt enkelt av att varje punkt är kompakt.

Ja, men efter detta skriver han

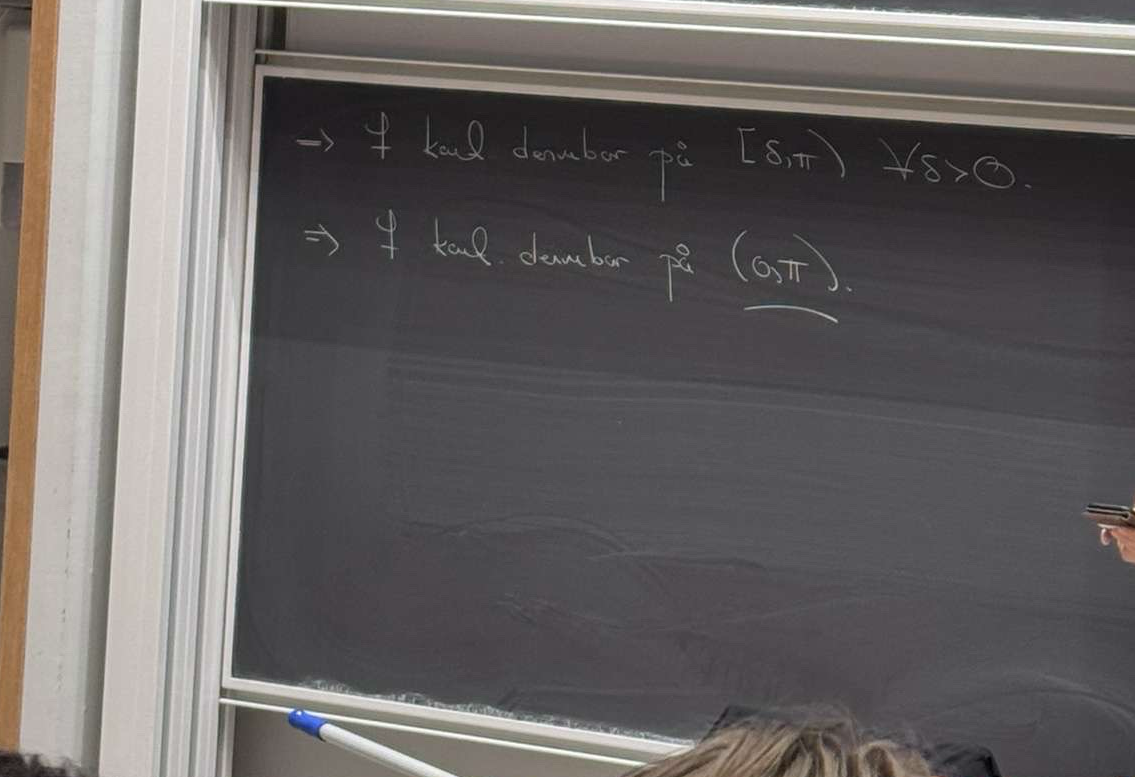
Detta är slutklämmen på 8 c) nedan. 

Det står att f är kontinuerligt deriverbar. Det är inte detsamma som likformigt kontinuerlig.

Inledningen till problemet saknas, men jag gissar att det man diskuterar är satsen som säger att:

1. Om en serie av kontinuerliga funktioner är likformigt konvergent så är gränsen kontinuerlig

2. Om funktionerna i serien är deriverbara så är gränsen deriverbar.

3. Gränsen KAN men MÅSTE INTE vara kontinuerlig resp deriverbar även utan likformig konvergens.

Det förstår jag. Satsen vi (och han) använder för att bevisa kontinuerlig deriverbarhet är

alltså 

-fn konvergerar punktvis

-fn är kontinuerligt deriverbar

-fn' konvergerar likformigt till g (det är detta steg han visar på sista tavlan där han också skrivit ner satsen märkte jag nu)

Bumpar denna.