Ett lugnande medel injiceras i en muskel - matte 3c
Hej! Har suttit och klurat på en fråga väldigt länge nu... vet inte riktigt vad det är jag har missat. Den lyder som följande:
Ett lugnande medel injiceras i en muskel varifrån det går ut i blodomloppet. Koncentrationen i blodet, y mg/liter, kan beskrivas med modellen: y = 0,7x * e^(-0.36x), där x är antalet timmar efter att injektionen givits. Det lugnande medlet är effektivt när koncentrationen i blodet är minst 0,4 mg/liter. ta reda på hur många timmar det lugnande medlet är effektivt enligt modellen. Svara med decimal.
Såhär har jag tänkt:
0,4 = 0,7x*e^(-0,36x)
0,4/0,7=x*e^(-0.36x)
ln(0,4/0,7)=x*lne*-0.36x
ln(0.4/0.7)=-0.36x^2
ln(0.4/0.7)/(-0.36)= x^2
1.5544... = x^2
x = +/- 1.2467... = 1.25 h
Svaret är dock 6,2 h... skulle verkligen upskatta hjälp!
Tack på förhand!
Välkommen till Pluggakuten!
Ser ut som att det blir något knas från rad 2 till 3.
Du har tänkt att ln(x*e^-(0.36x))=x*ln(e^-(0.36x)), det stämmer inte.
Däremot gäller att ln(x*e^-(0.36x)) = ln(x) + ln(e^-(0.36x))
Hej, tack! Och tack för svar! Fastnar dock fortfarande...
0,4 = 0,7x*e^(-0,36x)
0,4/0,7=x*e^(-0.36x)
ln(0,4/0,7)= ln(x*e^-(0.36x)) --> ln(x) + ln(e^-(0.36x))
ln(0.4/0.7)= ln(x) + (lne * -0.36x) --> ln(0.4/0.7) + 0.36x = ln(x)
ln(0.4/0.7) + 0.36x = ln(x)
e^(ln(0.4/0.7) + e^(0.36x) = e^(ln(x))
(0.4/0.7) + e^(0.36x) = x
Hur löser jag ut x i detta fall???
Vet fortfarande inte hur jag ska gå till väga :( Tack igen på förhand!
Den måste du lösa numeriskt eller grafiskt
Men svaret blir inte 6,2 utan lite mer.
Hej, varför kan man inte lösa den algebraiskt? Menas det att jag ska prova mig fram på ett x-värde för att få ett värde som närmar sig y = 0,4?
Antingen prova eller använda ngt digitalt hjälpmedel.
Har du skrivit av uppgiften rätt?
Frågan: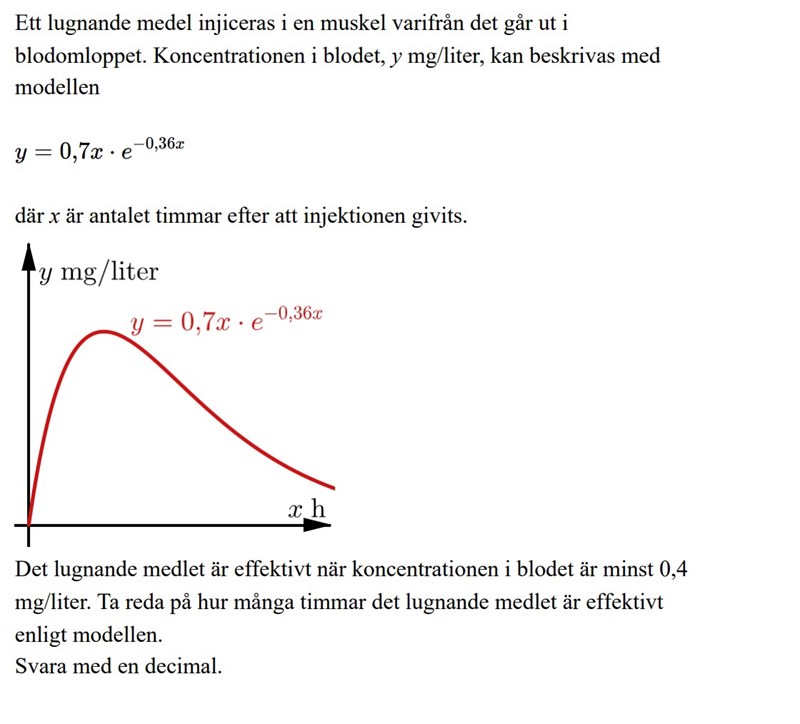
Tack igen.
ok,
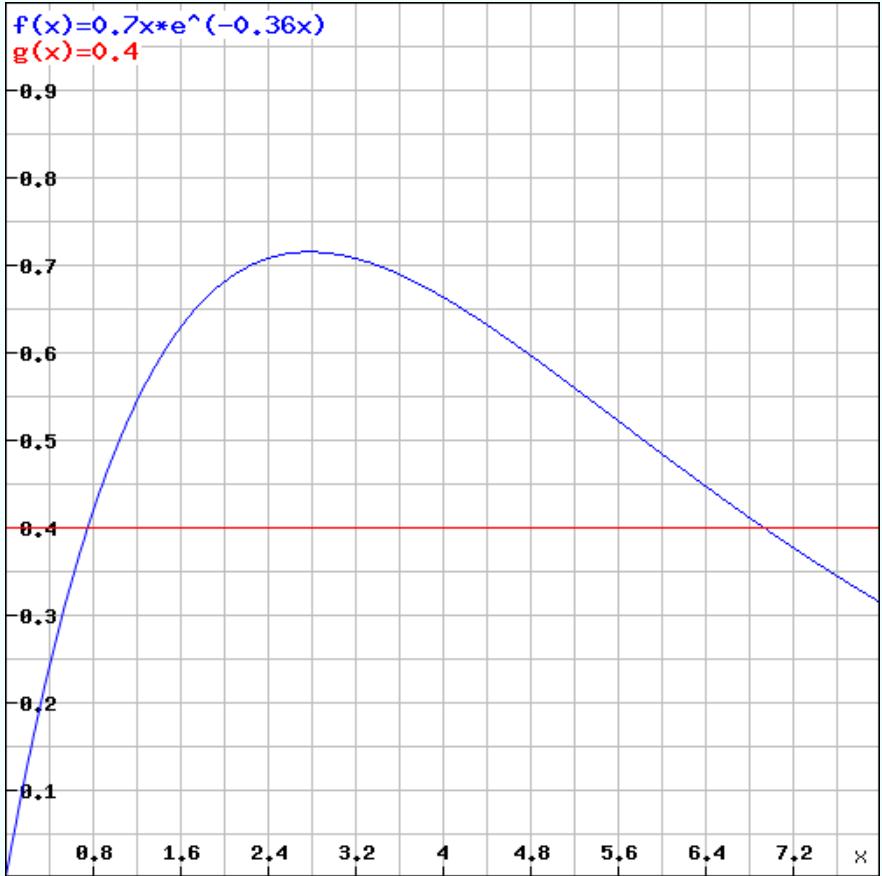
om du plottar funktionen och lägger in y = 0,4 får de en kurva enligt nedan.
Som synes är svaret inte 6,2 utan snarare 6,9.