Ett rymdfarkost
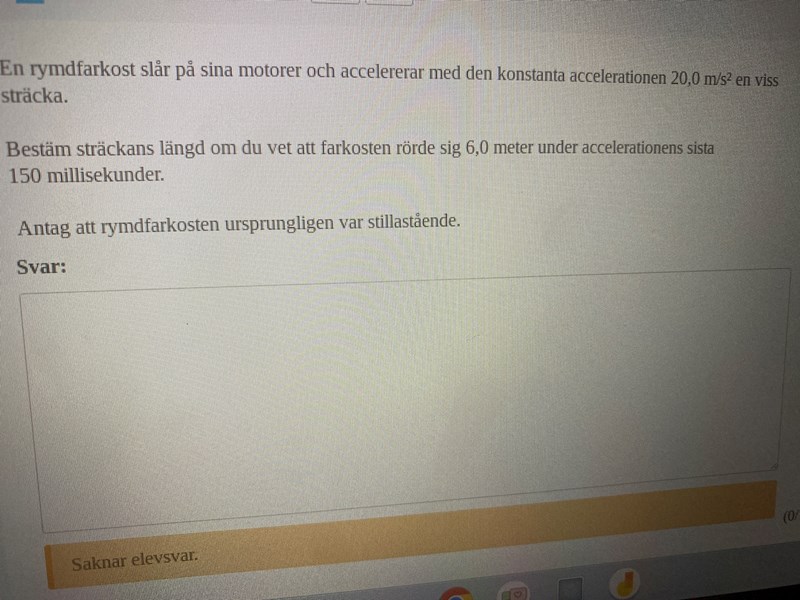
Hej! Jag förstår inte hur jag bör gå till vida när g löser denna fråga
Det är dom vanliga formlerna för rätlinjig rörelse som gäller.
du kan exvis räkna ut vilken hastighet den har precis innan de sista 6 metrarna
För att sedan räkna ut hur långt det är dit.
men på det sättet som jag räknar känns ändå rätt men kanske mittendelen är fel? Hur ska jag fortsätta utifrån det jag har skrivit?
Jag ser inget som du skrivit, är det i inlägg 2? I min dator är det inlägget tomt!
Jaha.
6=a•0,15^2/2
a=533,3
533•0,15=80 m/s
t= 80/20=4 s
Totalt 19 s
s=(20•19^2)/2
Något sådant skrev jag, lite slarvigare men aja
Äpple skrev:Jaha.
6=a•0,15^2/2
a=533,3
533•0,15=80 m/s
t= 80/20=4 s
Totalt 19 s
s=(20•19^2)/2
Något sådant skrev jag, lite slarvigare men aja
Jag tänker mig att vi tittar på de sista 6 metrarna, då har vi hastigheten f när vi börjar, tiden är 150 ms och vi använder sambandet
s = v0*t +at2/2 vilket ger oss ett värde på f (som motsvaras av v0 i formeln) . Som alltså är den hastighet vi har när det återstår 6 meter.
Sen kan vi använda sambandet
v2-v20 =2ax där v är sluthastighet, v0 är begynnelsehastighet, a är accelerationen och x är sträckan för att bestämma avståndet fram till den punkt där det återstår 6 meter. (observera att v0 inte är samma v0 som i förra formeln )
med v = det f vi räknade ut i förra formeln
v0 = 0
a = 20
x är det vi söker (så när som på 6 meter alltså)
men f är väl 0? Det finns ingen starthastighet
Äpple skrev:men f är väl 0? Det finns ingen starthastighet
Om du menar att hastigheten var 0 när t = 0 så stämmer det, men det är ju vid tidpunkten "150 ms innan accelerationen är klar" som vi vill ha hastigheten! Då är rymdfarkosten uppe i nästan hela sin totala hastighet.
Att rita en enkel skiss över situationen man ska räkna på och införa beteckningar för okända storheter underlättar tankearbetet något enormt.
Så här har jag skissat
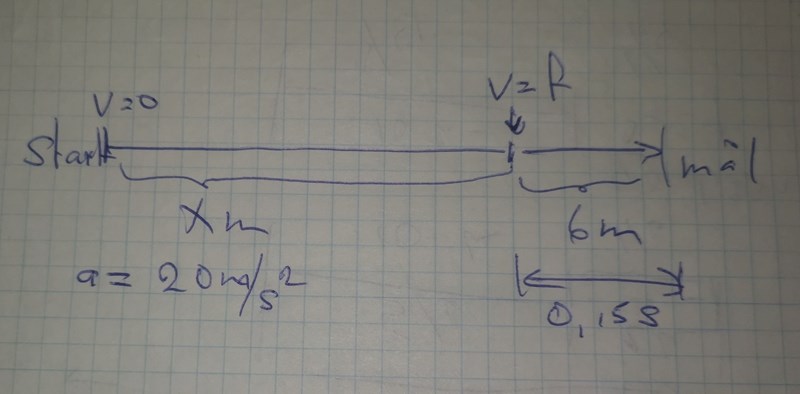Ta för vana att alltid rita en bild (något som på modernt snobbspråk kallas att visualisera) det tar inte mycket tid men det minskar risken för tankefel.
