Eulers fi funktion, en gång för alla!

2. φ(5p) = φ(5) + φ(p) = 4 + (p-1) = p + 3 blir då för mig: p=20 (eftersom 5*20=100), alltså 23? eller?

Vad har du för värde på p här?

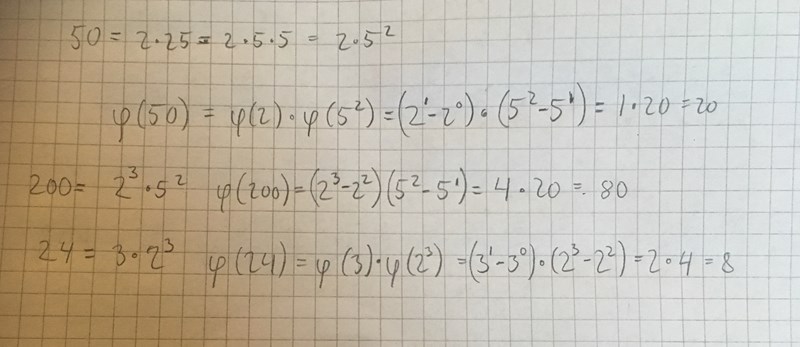Är inte helt säker på vad du frågar, men jag räknar ut det såhär. Hoppas du ser mönstret, fick inte ihop det i ord 😅. Tänk på att en multiplikativ funktion bara behöver vara det för tal som saknar genemsamma primfaktorer, annars kan lite vad som helst hända.

Smaragdalena skrev:

2. φ(5p) = φ(5) + φ(p) = 4 + (p-1) = p + 3 blir då för mig: p=20 (eftersom 5*20=100), alltså 23? eller?

Vad har du för värde på p här?

jag antar p=20, eftersom 5p=100?

Står inte p för primtal? Isf är 20 ett dåligt val.

Du skulle kunna titta på den engelska eller svenska wikipedia-sidan också. 

mrlill_ludde skrev:

Smaragdalena skrev:

Visa föregående citat

2. φ(5p) = φ(5) + φ(p) = 4 + (p-1) = p + 3 blir då för mig: p=20 (eftersom 5*20=100), alltså 23? eller?

Vad har du för värde på p här?

jag antar p=20, eftersom 5p=100?

Det står i förutsättningarna i satsen att OM p är ett tillräckligt stort primtal, så... Är 20 ett primtal? Kan man alltså använda satsen så som du har gjort?

Om $n$ är ett positivt heltal så betecknar $\phi(n)$ antalet positiva heltal (mindre än $n$) som är relativt prima med $n$; exempelvis är $\phi(10) = 4$ eftersom talen 1, 3, 7, 9 saknar gemensam delare med 10 (är relativt prima med 10).

Om $p$ är ett primtal så är alla positiva heltal (mindre än $p$) relativt prima med $p$, så för ett primtal är $\phi(p) = p-1$.

För varje positivt heltal $n$ gäller det att

    $k\cdot \frac{n}{\log\log n} < \phi(n) \leq n-1$

och det finns heltal där den övre gränsen antas (primtalen!) men det finns inte heltal där den nedre gränsen antas (eftersom den nedre gränsen är aldrig ett heltal), där $k$ är en viss positiv konstant.

Micimacko skrev:

Står inte p för primtal? Isf är 20 ett dåligt val.

Nvm

Om $m$ och $n$ är två positiva heltal så gäller det att

    $\phi(m\cdot n)=\phi(m)\cdot\phi(n)\cdot\frac{d}{\phi(d)}$

där $d$ betecknar den största gemensamma delaren till $m$ och $n$; om $m$ och $n$ är relativt prima är $d = 1$ och $\phi(1) = 1$ varför funktionen $\phi$ är multiplikativ då den appliceras på heltal som är relativt prima.

Exempelvis är $\phi(2\cdot 5) = \phi(2)\cdot \phi(5) \cdot \frac{d}{\phi(d)}$ men talen $2$ och $5$ är primtal och saknar därför gemensam delare, utom talet $1$ förstås vilket då blir den största gemensamma delaren till $2$ och $5$, vilket ger $\phi(2\cdot 5) = \phi(2)\cdot \phi(5).$ Då $2$ och $5$ är primtal gäller det att $\phi(2) = 2-1$ och $\phi(5) = 5-1$ vilket ger resultatet $\phi(10) = 4.$

Det är känt att mängden $M$ är en tät delmängd av det öppna intervallet $(0,1)$. Vad säger detta om funktionen $\phi$?

    $M = \{\frac{\phi(n)}{n}\,:\, n = 1,2,3,\ldots\}.$

Det beräknades att $\phi(10) = 4$. Finns det något annat positivt heltal med samma $\phi$-värde som $10$? 

Micimacko skrev:

Är inte helt säker på vad du frågar, men jag räknar ut det såhär. Hoppas du ser mönstret, fick inte ihop det i ord 😅. Tänk på att en multiplikativ funktion bara behöver vara det för tal som saknar genemsamma primfaktorer, annars kan lite vad som helst hända.

Så man primtalsfaktoriserar?

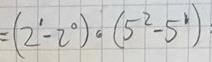
den e jag inte med på, vad e det för formel?

Albiki skrev:

Det beräknades att $\phi(10) = 4$. Finns det något annat positivt heltal med samma $\phi$-värde som $10$? 

kan det va alla multiplar?

mrlill_ludde skrev:

Albiki skrev:

Det beräknades att $\phi(10) = 4$. Finns det något annat positivt heltal med samma $\phi$-värde som $10$? 

kan det va alla multiplar?

Undersök själv. Är $\phi(10\cdot 2) = 4$? För beräkningen kan du utnyttja $10\cdot 2=4\cdot 5$; anledningen är att $4$ och $5$ är relativt prima, men $2$ och $10$ är det inte.