De Moivres formel?
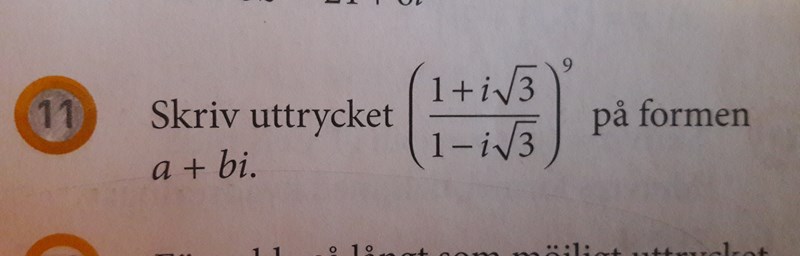 Hej!
Hej!
Jag tänker att jag kanske ska använda de Moivres formel för att lösa denna uppgift. Men jag vet inte hur jag ska börja ställa upp uttrycket .
Mycket tacksam för råd!
Börja med att förläng utrycket innanför parentessen med konjugatet till nämnaren för att få ett reelt tal i nämnaren.
Linn skrev:
Hej!
Jag tänker att jag kanske ska använda de Moivres formel för att lösa denna uppgift. Men jag vet inte hur jag ska börja ställa upp uttrycket .
Mycket tacksam för råd!
Ja du tänker rätt.
Skriv först både täljare och nämnare på polär form.
Använd sedan formeln för division av komplexa tal på polär form och till slut de Moivres formel.
Visa hur du försöker så hjälper vi dig om du kör fast.
Jag tycket att det verkar lättare att först få bort den imaginära delen i nämnaren så att det bara är täjlaren kvar att skriva om.
Tendo skrev:Jag tycket att det verkar lättare att först få bort den imaginära delen i nämnaren så att det bara är täjlaren kvar att skriva om.
Ja, det går att göra även på det sättet.
Okej så jag ska inte se hela uttrycket inom parentes som ett z?
Det är en smaksak om man gör sig av med nämnaren först och går över till polära koordinater sedan, eller om man börjar med att gå över till polära koordinater och utför divisionen sedan. Ni verkar rörande överens om att man skall se till att ha ett tal i polär form och sedan använda de Moivres formel.
Linn skrev:Okej så jag ska inte se hela uttrycket inom parentes som ett z?
Bara om du vill göra livet krångligt för dig själv. Ingen bra idé, om du frågar mig.
EDIT: Om du skriver om det till polär form - antingen på Yngves eller Tendos sätt - går det bra, men försök inte upphöja det som står i parentesen till 9 direkt!
Linn skrev:Okej så jag ska inte se hela uttrycket inom parentes som ett z?
Jo, om du ska använda de Moivres formel så är det bra att göra det.
Då gäller ju nämligen att och .
Så du bör skriva detta på polär form först. Du känner väl till polär form?
Följ de steg som jag tipsade om (eller de som Tendo tipsade om) så ska du se att det går bra.
Där behöver du känna till hur man dividerar komplexa tal på polär form.
Och sedan på slutet behöver du omvandla till rektangulär form.
Visa dina uträkningar så hjälper vi dig om du kör fast.
 såhär löste jag det
såhär löste jag det
1 är rätt enligt facit men jag undrar om mina uträkningar är korrekta?
Linn skrev:1 är rätt enligt facit men jag undrar om mina uträkningar är korrekta?
Nej ditt är fel.
Eftersom tangens har periodicitet så måste du ta hänsyn till vilken kvadrant ligger i.
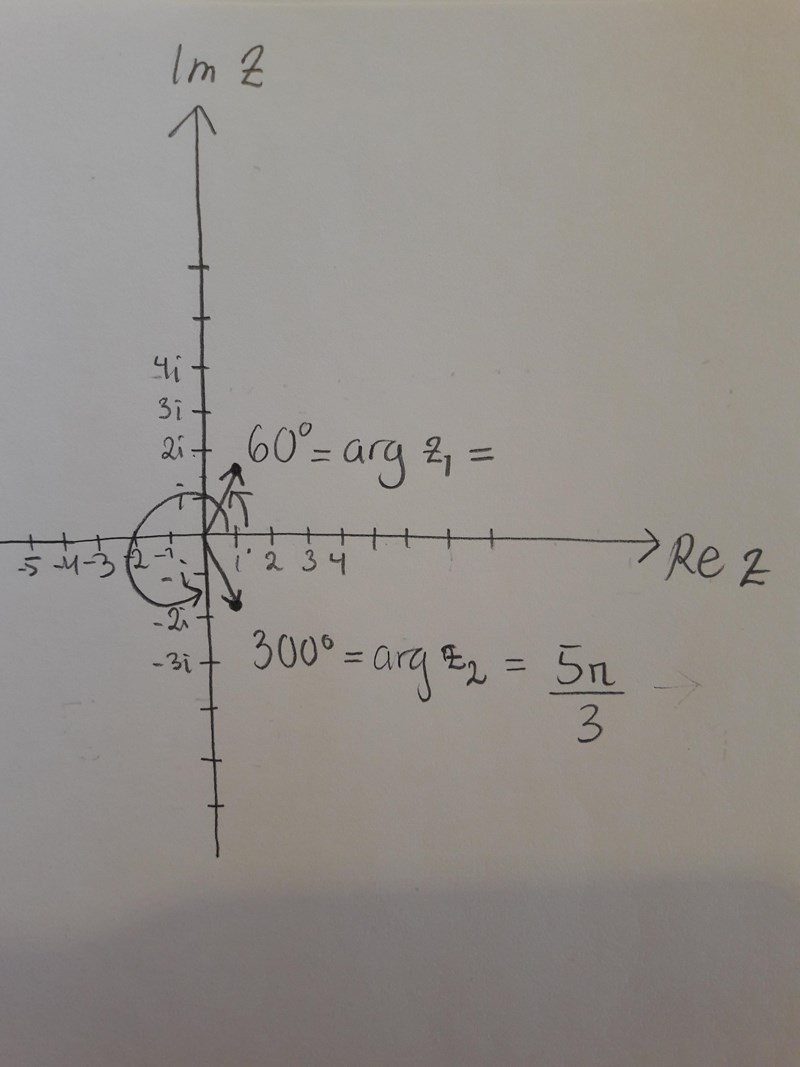
Börja alltid med att göra en enkel figur. Markera och i det komplexa talplanet innan du översätter till polär form.
Du har mycket större chans att få rätt svar om du följer råden du får och beräknar innan du använder de Moivres formel. Du har också använt en del alternativa fakta när det gäller trigonometriska formler. Vad sysslar du med när du går från näst sista till sista raden? Cosinus och sinus för något ligger alltid mellan -1 och 1, det kan aldrig bli 2, och vart tog vägen?
Jag förstår inte felet med argz2..
Linn skrev:Jag förstår inte felet med argz2..
Om du ritar en figur så förstår du nog vad som är fel.
Markera (ungefärligt) och i det komplexa talplanet och visa din figur.
Jag ser nu att argz2 ska vara pi/3.
Men när jag sedan multiplicerar in potensen 9 så får jag ju 9pi/3. När jag förkortar det får jag 3pi
Linn skrev:Jag ser nu att argz2 ska vara pi/3.
Men när jag sedan multiplicerar in potensen 9 så får jag ju 9pi/3. När jag förkortar det får jag 3pi
Nej det är som har argumentet . De två talen har inte samma argument.
Varför vill du inte visa din figur?
Linn skrev:Jag ser nu att argz2 ska vara pi/3.
Men när jag sedan multiplicerar in potensen 9 så får jag ju 9pi/3. När jag förkortar det får jag 3pi
Du kan inte ha ritat. Då skulle du se att hamnar i fjärde kvadranten. Vad blir argumentet?
Ja, eller .
Linn skrev:
OK bra.
Jag skulle också använda för att få enklare beräkningar.
Sen är det bara att köra vidare från steget "arg =" i din uträkning.
Men som Smaragdalena påpekade, kolla en extra gång på den avslutande omvandlingen till rektangulär form.