Eulers metod: Tolkning av uppgift

Förlåt för den vaga titeln men jag har problem med att tolka en viss uppgift som involverar approximation med Eulers metod. Uppgiften lyder:

Specifikt Uppgift B. Uppgift A har jag gjort, var jag skapat en funktion f(x) var $f (x) = \frac{x}{3}$ om $x < 75$ (annars returnerar f(x) talet 25). Men i uppgift B så blir jag lite förvirrad. Jag förstår knappt vad det är jag ska göra eller hur jag ska börja. Jag vet inte heller riktigt om uppgift A och uppgift B är menade att hänga ihop eller om dem är oberoende av varandra.

Informationen i uppgift B som jag har fått är ett system av två diffekvationer:

${x_{i}}^{n + 1} = {x_{i}}^{n} + h * f ({x^{n}}_{i + 1} - {x^{n}}_{i}) o c h {x_{M}}^{n + 1} = {x_{M}}^{n} + h * g ({x^{n}}_{M})$

men dessa verkar bara vara omskrivna versioner av Eulers metod och ser inte ut som några vanliga diff.ekv jag stött på (Eulers metod: $y^{'} (x_{n + 1}) \approx y (x_{n}) + h * y^{'} (x_{n})$ ).

Var kommer f(x) och g(x) ifrån? Hur löser jag system av diff.ekv med Eulers metod (aldrig stött på detta tidigare)? Vad är mitt begynnelse värde (då t=0)? Varför är g definierad som en konstant (g=5m/s) i uppgift B1 men som en funktion i systemet av diff.ekv (och hur har jag någon användning av konstanten)? Eh... jag kan fråga minst 200 frågor till angående Uppgift B men poängen är att jag är förvirrad och har ingen aning var jag ska börja. Vet inte om jag är dum i huvudet eller om uppgiften är dåligt formulerad.

Jag har redan definierat en funktion i MATLAB som ska ge en Euler approximering (första ordningen) givet en funktion 'f', men förstår inte vad min funktion 'f' ska vara (f:et i $y^{'} (x_{n + 1}) \approx y (x_{n}) + h * f$ ) eller vad mitt begynnelsevärde ska vara (y(0) = ?).

Förlåt om jag bara babblar nonsens eller repeterar saker just nu men vill bara att någon förklarar meningen med Uppgift B på ett mer begripligt sätt.

Tack!

Din bild är så suddig att den inte är läsbar. Skriv av uppgiften ord för ord, så är det lättare att hjälpa dig. /moderator

Jag kunde läsa den, genom att ta bilden i en egen flik och använda Ctrl-+. Men det är sant att den är suddig.

b hänger ihop med a. Du ska stega fram systemet bit för bit med Euler-ekvationerna. De diff-ekvationer som det rör sig om är bara typ y'(x) = f(x). Så det är bara: bil 4 har hastigheten si och så (som ges av avståndet till bil 3) och då vet vi dess position h sekunder senare. Osv. Bil M kör på med konstant hastighet, säger du, men jag ser inte det i bilden. Om man låter den göra komplicerade saker blir det nån generell funktion g, så de har bara förberett för det. f är den som anges av kurvan och som du har definierat i Matlab. Var allt börjar står inte, men du kan ju anta att de står med 10 m mellanrum och står stilla och sedan M börjar köra, så ska till slut allt ringla iväg. Står det vad h ska vara? Ta nåt bra annars, t.ex. 0,1 s.

Aha, jag missade andra sidan, där står att g är 5 m/s.

Smaragdalena skrev:
Din bild är så suddig att den inte är läsbar. Skriv av uppgiften ord för ord, så är det lättare att hjälpa dig. /moderator

Konstigt... jag kan se texten helt utan problem. Har du testat att öppna bilden i en ny flik och zooma in? Jag skriver väl ner den som text om någon annan klagar på detta också...

Begynnelsevärdena verkar stå där också.

Laguna skrev:
Jag kunde läsa den, genom att ta bilden i en egen flik och använda Ctrl-+. Men det är sant att den är suddig.

b hänger ihop med a. Du ska stega fram systemet bit för bit med Euler-ekvationerna. De diff-ekvationer som det rör sig om är bara typ y'(x) = f(x). Så det är bara: bil 4 har hastigheten si och så (som ges av avståndet till bil 3) och då vet vi dess position h sekunder senare. Osv. Bil M kör på med konstant hastighet, säger du, men jag ser inte det i bilden. Om man låter den göra komplicerade saker blir det nån generell funktion g, så de har bara förberett för det. f är den som anges av kurvan och som du har definierat i Matlab. Var allt börjar står inte, men du kan ju anta att de står med 10 m mellanrum och står stilla och sedan M börjar köra, så ska till slut allt ringla iväg. Står det vad h ska vara? Ta nåt bra annars, t.ex. 0,1 s.

Vet inte om du är bekant med MATLAB kod men här är vad jag har hittils (för inbromsningsdelen):

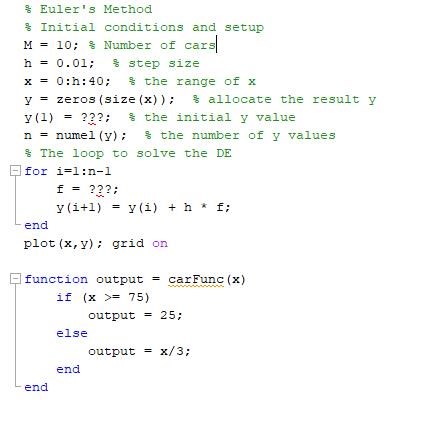
Jag vet inte riktigt vad 'f' ska vara här. Är 'f' menad att vara 'carFunc'? Vad ska 'carFunc' då ha för parameter (avståndet mellan två bilar eller?). Begynnelsevärdet 'y(1)' kan jag inte heller riktigt klura ut (ska det vara $x_{i} (0) = d * i$ som ges i Inbromsningssektionen av uppgiften? d=75 från uppgift A). 'M' (antalet bilar) är just nu oanvänd. Eftersom att M inte används just nu och varje bil har ett index så säger det mig att Eulerfunktionen i koden ska utföras en gång PER bil, alltså totalt 10 gånger (dvs. koden i bilden ska sättas i en yttre for-loop som loopar 10 gånger). Måste 'x' och 'y' vara matriser då istället för vektorer (eftersom att dem då måste ha 2 indexar, yttre-loop och inre-loop). Är jag på rätt spår eller är jag helt ute och cycklar?

Hoppas att du förstår MATLAB annars verkar jag som en galning när jag försöker förklara detta haha :)

EDIT: Hur kommer g=5m/s och systemet av diff.ekv in i bilden egentligen?

g säger hur den första bilen rör sig.

Laguna skrev:
g säger hur den första bilen rör sig.

Oj! Jag råkade läsa det som "Låt bilarnas HASTIGHETER vid tiden t=0 ges av..." istället för "Låt bilarnas POSITIONER vid tiden t=0 ges av...". Inte konstigt att jag blev förvirrad över vad poängen med 'g' var haha! :D

Hej!

Om avståndet mellan två bilar är litet så kan du linjärisera bilarnas hastigheter $f$ kring origo.

$f(x_{i+1}-x_{i}) \approx f(0) + f'(0)\cdot (x_{i+1}-x_{i})$

vilket ger dig ett linjärt ekvationssystem för att bestämma positionerna hos alla bilar, utom för ledarbilen (vars hastighet styrs av funktionen $g$ ).

$\mathbf{x}_{n+1} = \mathbf{x}_{n} + h \cdot f(0) \mathbf{1} + h \cdot f'(0) A_{n}$

där matrisen $A_{n}$ är av typ $(M-1)\times (M-1)$ och består av 1:or och -1:or.

Svara

Visa senaste svar