evaluate the line integral
Hej! Jag undar hur de kom fram till vad r(t) var och varför blir det t^2(2t) inanför integralen?
Tack på förhand!
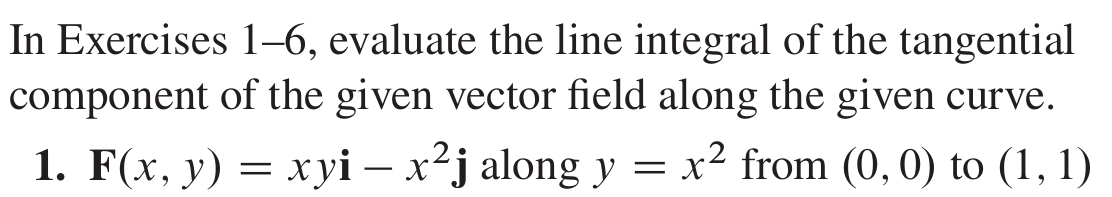
Facit:
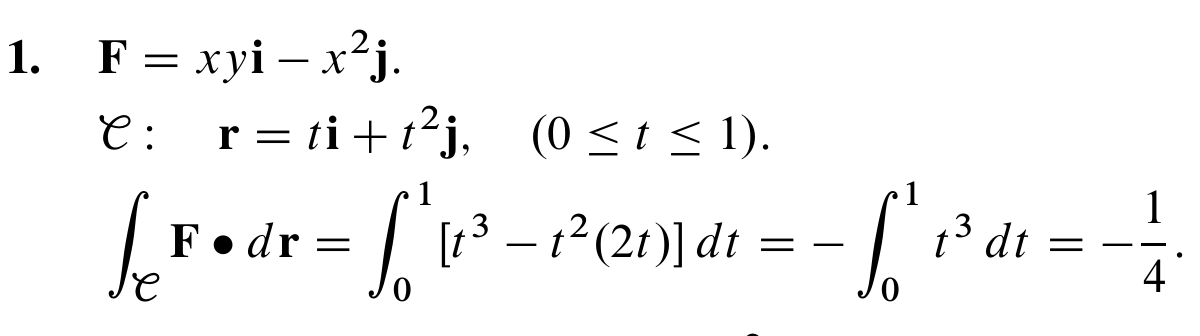
Min lösning:
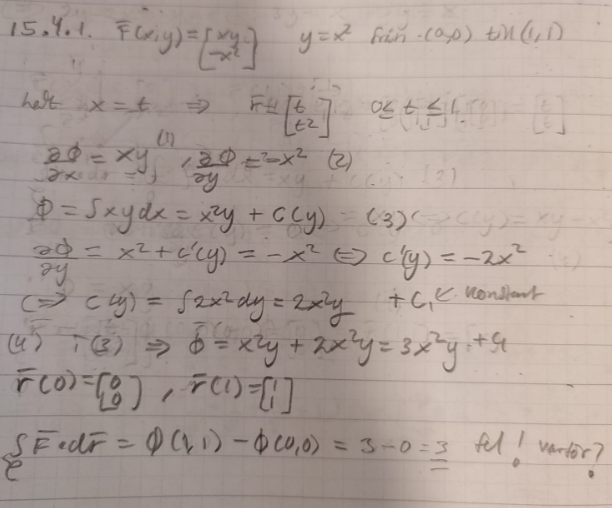
Så här gjorde jag och fick till viss förvåning samma som facit. Jag ska titta på din lösning

Nej, jag påstår varken att du gör fel eller rätt, jag bara förstår inte din lösning. Andra som är bättre på kurvintegraler än jag får ta över.
r (t) är (t, t2) eftersom kurvan är y = x2
dr/dt är (1, 2t)
så vi beräknar integralen F dr = F dr/dt dt
Kanske omatematiskt men så tänker jag.
Sedan tycker jag det är mycket tydligare att skriva som kolonnvektorer än att tôla med i och j.
En potentialfunktion kan du bara använda om fältet är konservativt, har du kollat det? Alltså att . Både Marilyn och facit använder definitionen av kurvintegral:
där kurvan parametriserats med en funktion där .
Tillägg: 5 maj 2025 16:31
Hur gör jag så att mina integraler blir snygga men ej parenteserna förstörs med "\displaystyle"?
MrPotatohead skrev:Hur gör jag så att mina integraler blir snygga men ej parenteserna förstörs med "\displaystyle"?
Skriv: "\left("
Pieter Kuiper skrev:MrPotatohead skrev:Hur gör jag så att mina integraler blir snygga men ej parenteserna förstörs med "\displaystyle"?
Skriv: "\left("
Där ja, tackar.
Tack så mycket för alla svar! Jag hade inte kontrollerat om fältet var konservativt, gjorde det nu och det var inte konservativt, nu förstår jag hur factit och marilyn gjort! Tack!:)





