Evaluate the line integral of the tangential component of vector field

Parametriseringen ser rätt ut och man kan dubbelkolla genom att plotta den i geogebra:

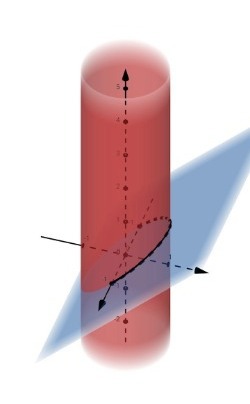
Det verkar rätt att sätta gränserna $t\in[0,\pi]$.

Sedan är inte den där integralen så farlig. Trixa lite så ser du nog några knep.

 Uppgiften säger att det inte spelar någon roll åt vilket håll kurvan går. Det är nästan en ledtråd till att fältet är konservativt och det finns en potentialfunktion f(x,y,z) , (vilket det finns, jag har kollat).

Då är ju integralen f(ändpunkt) - f(startpunkt)

Det är nog enklaste sättet. (om du vet hur man hittar potentialfunktioner).

jamolettin skrev:

 Uppgiften säger att det inte spelar någon roll åt vilket håll kurvan går. Det är nästan en ledtråd till att fältet är konservativt och det finns en potentialfunktion f(x,y,z) , (vilket det finns, jag har kollat).

Då är ju integralen f(ändpunkt) - f(startpunkt)

Det är nog enklaste sättet. (om du vet hur man hittar potentialfunktioner).

Om vi inte visste att vfältet var konservativt kan vi kolla det snabbt genom $\nabla \times \textbf{F}=0$ vilket verkar stämma tillsammans med faktumet att vfältet är enkelt sammanhängande som medför att  F är konservativt. Så arbetet = integralen av $\textbf{F} \cdot  d\textbf{r}=0$.

Kan man enkelt tänka att eftersom vi startar och slutar på samma position i just z-led så blir arbetet alltid 0?

Nej, inte generellt. Integralen av F*dr blir inte noll bara för att fältet är konservativt, den blir noll om det är en sluten kurva (och konservativt fält). I det här fallet är ju inte kurvan sluten.  
Att din integral blir noll är mer av en tillfällighet, det beror på hur vektorfältet ser ut.

edit: Potentialfunktionen blir x*y*z vilken kommer ha värdet noll om någon av x,y,z är noll.

jamolettin skrev:

I det här fallet är ju inte kurvan sluten.  

Så hur ser du då att arbetet blir 0? (Att säga arbetet blir 0 är väl synonymt med att integralen av $F \cdot dr=0$?)

Jag ser att integralen blir noll genom att beräkna potentialfunktionen, jag kallar den för f(x, y, z)=x*y*z

Integralen av F*dr = f(1,0,0) - f(-1,0,0)

= 1*0*0 - (-1)*0*0 = 0

Edit

Du måste alltså ta reda på potentialen först. 

Vilket är relativt enkelt i det här fallet. 

Om du inte har gjort det tidigare antar jag att du löser den på det andra sättet som du började med. 

jamolettin skrev:

Jag ser att integralen blir noll genom att beräkna potentialfunktionen, jag kallar den för f(x, y, z)=x*y*z

Integralen av F*dr = f(1,0,0) - f(-1,0,0)

= 1*0*0 - (-1)*0*0 = 0

Edit

Du måste alltså ta reda på potentialen först. 

Vilket är relativt enkelt i det här fallet. 

Om du inte har gjort det tidigare antar jag att du löser den på det andra sättet som du började med. 

Okej jag tror jag är med nu. Du vet att $\int F \cdot dr$ är lika med potentialen till F eftersom F är konservativt? Och att integralen och gradienten tar ut varandra, vilket lämnar oss med potentialen?

Jag skulle snarare uttrycka mig så här (men det är kanske det du menar?):

Om alla villkor är uppfyllda (kolla upp dem) så gäller:

Antag att U är en potential till vektorfältet F,  då gäller grad(U)=F

och kurvintegralen av F längs en kurva C är lika med U:s värde i kurvans ändpunkt minus U:s värde i kurvans startpunkt.

jamolettin skrev:

Jag skulle snarare uttrycka mig så här (men det är kanske det du menar?):

Om alla villkor är uppfyllda (kolla upp dem) så gäller:

Antag att U är en potential till vektorfältet F,  då gäller grad(U)=F

och kurvintegralen av F längs en kurva C är lika med U:s värde i kurvans ändpunkt minus U:s värde i kurvans startpunkt.

Tack för sammanfattningen. Ska spara detta!