13 svar

2887 visningar

Nide behöver inte mer hjälp

Exakt bakåt-Euler lösning

Jag håller på och gör en skoluppgift som går ut på att lösa differentialekvationer med Euler's metod "för en modell av förarlösa bilar" och har en deluppgift som lyder:

(har markerat den viktiga delen av deluppgiften med gul färg, ignorera resten)

Detta kanske är lite förvirrande så här är också lite kontext till uppgiften så ni får en större bild över det hela:

(Deluppgift 'a' och 'b' har jag redan gjort. Inkluderade bara dessa pga kontext)

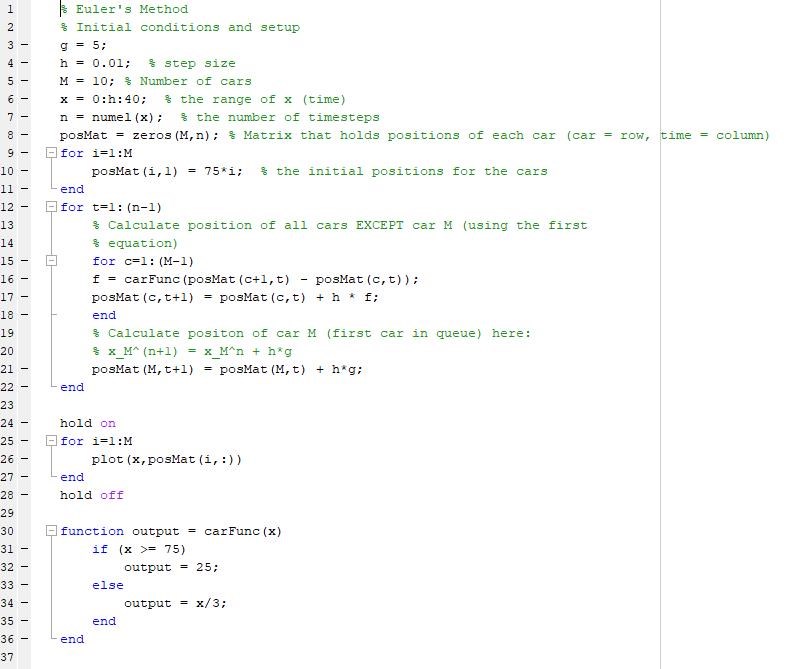
Här är min nuvarande (trasiga) MATLAB kod för deluppgift 'h':

Bakåt-Euler betecknas som $y_{k + 1} = y_{k} + h f (t_{k + 1}, y_{k + 1})$ och min tolkning av en "exakt bakåt-Euler" lösning är att man skriver om ekvationen ovanför som en ekvation var det inte finns några $y_{k + 1}$ i högerledet (dvs, man flyttar alla $y_{k + 1}$ till vänsterledet). Bakåt-Euler representeras i min kod av rad 16 och 17. Jag tänker mig att "posMat(c,t+1)" i min kod representerar $y_{k + 1}$ i detta fall. Problemet är att jag inte vet vad "posMat(c+1,t+1)" representerar. Hur blir blir jag av med "posMat(c+1,t+1)" eller hur hanterar jag detta värde? Den representerar väl tekniskt sett också $y_{k + 1}$ fast för en helt annan bil i matrisen. Eller?

Hjälp!

(Förlåt för den långa texten. Jag kände att denna uppgift krävde lite extra kontext för att förstå vad jag pratar om. Förlåt också om min förklaring av problemet är lite flumming. Fråga gärna om någonting är oklart :) )

Nu gissar jag hejvilt. Men jag tror att med exakt Euler bakåt ska du använda uttrycket för bakåt Euler som innehåller integralen av derivatan av y. Kolla på wikipedia https://en.wikipedia.org/wiki/Backward_Euler_method . I deriveringen av bakåt Euler används i ett steg integralen. Om y' är känd och enkel att integrera blir det ett exakt svar. Gör som i deluppgift b) och skriv y' som en matlabfunktion som matlab kan integrera.

Aerius skrev:
Nu gissar jag hejvilt. Men jag tror att med exakt Euler bakåt ska du använda uttrycket för bakåt Euler som innehåller integralen av derivatan av y. Kolla på wikipedia https://en.wikipedia.org/wiki/Backward_Euler_method . I deriveringen av bakåt Euler används i ett steg integralen. Om y' är känd och enkel att integrera blir det ett exakt svar. Gör som i deluppgift b) och skriv y' som en matlabfunktion som matlab kan integrera.

Jag antar att du menar denna ekvation:

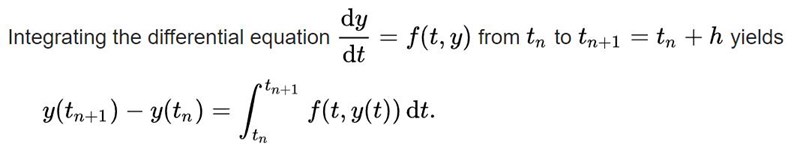
Om man översätter detta till (min) kod så tror jag att man får någonting i stil med:

posMat(c,t+1) - posMat(c, t) = integral(func, t, t+1)

Jag förstår att "func" i detta fall ska vara derivatan av "y", men mitt "y" i detta fall är en matris och inte en funktion. Hur hittas jag då derivatan av "y" för att få "f(t, y)"?

Vill också veta vad skillnaden är mellan skillnaden är mellan $y (t_{n})$ , $y (t)$ och bara $y$ i ekvationen (t.ex. i ekvationen finns både $f (t, y)$ och $f (t, y (t))$ . Betyder dem samma sak? Finns det en skillnad?).

Förlåt om vissa frågor är väldigt dumma. Jag är bara riktigt förvirrad över detta.

Nu har jag funderat lite till. Jag kan ha fel för det här var längesedan. Men när jag tittar på rad 17 till 21i din kod. Så tror jag att det du ska göra är istället för att beräkna $h * f$ och $h * g$ ska du beräkna $\int_{t_{n}}^{t_{n + 1}} f d t$ och $\int_{t_{n}}^{t_{n + 1}} g d t$ . Borde inte din funktion $f$ ge samma resultat som $f$ i deluppgift a) ?

Om man vet att $y$ beror av $t$ är det ingen skillnad att skriva $y (t)$ eller $y$ . Att skriva $y (t)$ gör det bara tydligare att $y$ är en funktion av $t$ . Att det står $y (t_{n})$ betyder att $t$ är diskret (till exempel $t_{1} = 0, t_{2} = 3 . . .$ osv), $y$ är fortfarande en funktion av $t$ .

(Tomt inlägg)

Hej!

På rad 8 står det vad posMat representerar: "Matrix that holds positions of each car (car = row, time = column)".

Då det finns $M$ stycken bilar vars positioner studeras vid $n$ stycken tidpunkter är posMat en matris av typ $M\times n$ . Matrisen initieras som en nollmatris för att så småningom fyllas med meningsfullt innehåll.

På rad 10 fyller man i de $M$ bilarnas startpositioner (75, 75*2, 75*3 , ... 75*M) vilka placeras i matrisens första kolumn.

Albiki skrev:
Hej!
På rad 8 står det vad posMat representerar: "Matrix that holds positions of each car (car = row, time = column)".
Då det finns $M$ stycken bilar vars positioner studeras vid $n$ stycken tidpunkter är posMat en matris av typ $M\times n$ . Matrisen initieras som en nollmatris för att så småningom fyllas med meningsfullt innehåll.
På rad 10 fyller man i de $M$ bilarnas startpositioner (75, 75*2, 75*3 , ... 75*M) vilka placeras i matrisens första kolumn.

Jag vet det. Jag skrev den koden och kommentarerna. Koden i bilden är en kopia av min kod i uppgift 'b' men nu försöker jag anpassa den så att den passar uppgiften i uppgift 'h'. Jag har dock problem med att förstå exakt vad som menas med "Ett EXAKT uttryck för en båkat-euler lösning" (texten som jag har markerat med gul färg i toppen av inlägget). Med andra ord, hur anpassar jag rad 16, 17 och 21 så att dem uppfyller uppgiften i uppgift 'h'?

Här är min (fungerande) kod från Uppgift 'b' som istället använder framåt-euler metoden (för referens):

Du skrev faktiskt att "Problemet är att jag inte vet vad "posMat(c+1,t+1)" representerar." men nu skriver du att du vet detta, så mitt inlägg var helt onödigt?

Aerius skrev:
Borde inte din funktion $f$ ge samma resultat som $f$ i deluppgift a) ?

Det gör den. Har dock skrivit om den lite i uppgift H (men misslyckats). Kolla på koden jag la upp i svaret till Albiki ovanför. Det är en fungerande version av koden och den kanske ger dig en lite större överblick. Fast den använder istället framåt-Euler (jag har också skrivit en lösning för bakåt-euler, som jag inte lagt upp, men den använder fixpunktsmetoden, vilket betyder att det inte är en EXAKT bakåt-euler lösning utan bara en approximation).

Albiki skrev:
Du skrev faktiskt att "Problemet är att jag inte vet vad "posMat(c+1,t+1)" representerar." men nu skriver du att du vet detta, så mitt inlägg var helt onödigt?

Jag ser hur man kan ha missförstått detta. Vad jag menade var att jag inte fattade vad "posMat(c+1, t+1)" representerade i relation till den generella ekvationen för bakåt-Euler $y_{k + 1} = y_{k} + h f (t_{k + 1}, y_{k + 1})$ . Alltså t.ex., jag vet att $y_{k + 1} = p o s M a t (c, t + 1)$ och $y_{k} = p o s M a t (c, t)$ . Men vad är då "posMat(c+1, t+1)"? Hur passar den biten av koden in i ekvationen?

EDIT: Alltså, så som jag har förstått så måste jag skriva om koden/ekvationen "posMat(c, t+1) = posMat(c, t) + h*(posMat(c+1, t+1) - posMat(c, t+1)/3)" så att alla posMat(c, t+1) flyttas över till vänsterledet. Då får jag en exakt bakåt-euler lösning (så har jag tolkat det i alla fall). Men vad gör jag med "posMat(c+1, t+1)"? Den kan inte vara kvar i högerledet för då kan jag inte räkna ut bakåt-euler eftersom att värdet av "posMat(c+1, t+1)" är värdet av "tidssteget i framtiden". Jag vet bara vad värdet av "posMat(c, t)" är i tidspunkten 't'. Sorry om jag förklarar detta dåligt. Vet inte riktigt hur jag ska förklara det.

Nu föll polletten ner. För detta problem går det att hitta en exakt lösning på Euler bakåt med hjälp av penna och papper. Alltså du ska skriva ner ekvationssystemet och lösa ut $x^{n + 1}$ givet $x^{n}$ . Då får du en exakt lösning till bakåt Euler. Jämför denna exakta lösning $x^{n + 1}$ med den numeriska beräkningen av bakåt Euler. Det står på raden före det gulmarkerade. Jag var totalt ute och cyklade med integralen av derivatan av y.

Aerius skrev:
För detta problem går det att hitta en exakt lösning på Euler bakåt med hjälp av penna och papper. Alltså du ska skriva ner ekvationssystemet och lösa ut $x^{n + 1}$ givet $x^{n}$ . Då får du en exakt lösning till bakåt Euler.

Jag antar att du menar ekvationssystemet '(4)' i uppgift 'b'. Då får jag:

$\{\begin{cases} {x^{n + 1}}_{i} = {x^{n}}_{i} + h f ({x^{n + 1}}_{i + 1} - {x^{n + 1}}_{i}) \\ {x^{n + 1}}_{M} = {x^{n}}_{M} + 5 h \end{cases}$

(eftersom att 'g' är 5 i inbromsningsfallet)

Eftersom att funktionen är $f (x) = \frac{x}{3}$ (enligt uppgift 'a' [och $f (x) = 25$ om $x \geq 75$ ]) så får jag:

$\{\begin{cases} {x^{n + 1}}_{i} = {x^{n}}_{i} + h (\frac{{x^{n + 1}}_{i + 1} - {x^{n + 1}}_{i}}{3}) \\ {x^{n + 1}}_{M} = {x^{n}}_{M} + 5 h \end{cases}$

Den nedre ekvationen behöver jag inte göra någonting åt eftersom att jag inte har några okända i högerledet men i den övre ekvationen har jag två okända i högerledet ( ${x^{n + 1}}_{i + 1}$ och ${x^{n + 1}}_{i}$ ). Jag vet att jag kan flytta över ${x^{n + 1}}_{i}$ till högerledet men vad gör jag med ${x^{n + 1}}_{i + 1}$ ? Den är också okänd och så länge den finns i mitt högerled så kan jag inte räkna ut vad ${x^{n + 1}}_{i}$ blir. Det är här själva problemet ligger. Det är det här jag har svårt att förstå.

Jämför denna exakta lösning $x^{n + 1}$ med den numeriska beräkningen av bakåt Euler.

Hur kom du till den slutsatsen? I den gulmarkerade texten står det att jag ska konvertera den EXAKTA bakåt-euler lösningen som jag fick med papper och penna till ett MATLAB program. Det står ju till och med senare i texten att jag ska plotta skillnaden av Euler-approximation (som jag har MATLAB kod av) med min exakta bakåt-euler lösning.

Det stod i uppgiften att jämföra den exakta bakåt Euler lösningen med fixpunkts iterationsfelet. Det går alltså att lösa bakåt Euler exakt med penna och papper. Sen ska du använda fixpunkts iterations metoden för att hitta $x^{n + 1}$ med bakåt Euler. Jämför sedan felet som uppstår när du använder fixpunktsmetoden mot när du använder den exakta lösningen.

Om inte det här fungerar då har jag ingen aning om hur problemet ska lösas.

Edit: Detta inlägg har blivit ändrat flera gånger.

Aerius skrev:
Det stod i uppgiften att jämföra den exakta bakåt Euler lösningen med fixpunkts iterationsfelet. Det går alltså att lösa bakåt Euler exakt med penna och papper. Sen ska du använda fixpunkts iterations metoden för att hitta $x^{n + 1}$ med bakåt Euler. Jämför sedan felet som uppstår när du använder fixpunktsmetoden mot när du använder den exakta lösningen.
Om inte det här fungerar då har jag ingen aning om hur problemet ska lösas.
Edit: Detta inlägg har blivit ändrat flera gånger.

Det är lugnt. Jag har löst det. Det visar sig att det är jag som är helt dum i huvudet. Värdet "posMat(c+1, t+1)" visade sig vara ett känt värde trots allt. Inte okänt som jag trodde från början. Så jag behövde inte egentligen göra någonting förutom att skriva om högerledet och flytta "posMat(c, t+1)" till vänsterledet. Jag hade löst uppgiften från första början och inte ens insett det -__-.

Här är den slutgiltiga MATLAB koden om någon är intresserad:

Svara

Visa senaste svar