Exponentialekvation
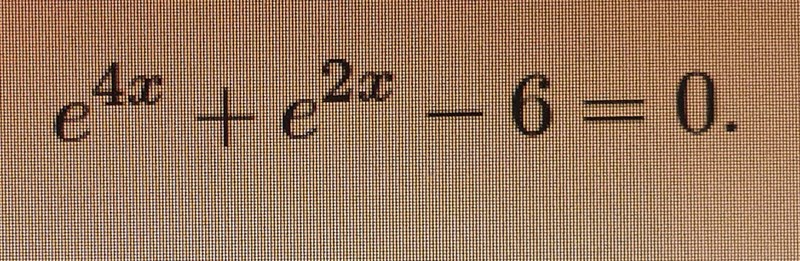
Svaret skall bli Har sett en lösning på denna, och då substituerade man ut till u och löser med pq. Men behövs det verkligen ?
Känner att jag behöver lite repetition.
Vad missuppfattar jag här ?
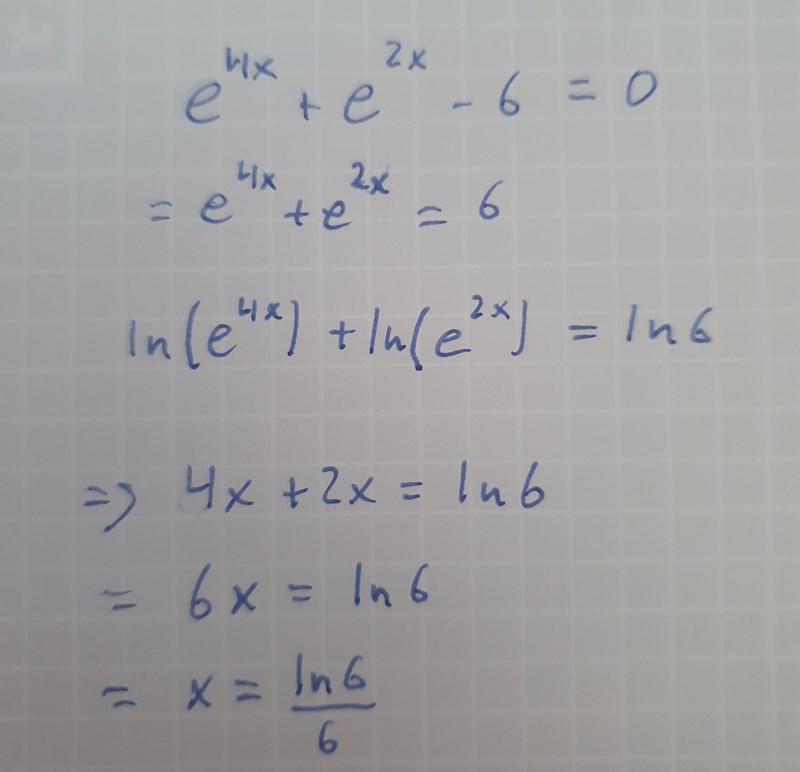
I dina uträkningar blev det lite fel när du applicerar ln[ ... ] på båda sidor.
ln[ a + b ] är inte samma som ln[a] + ln[b]. Det är ln[a * b] som motsvarar ln[a] + ln[b]
Så approachen med pq är inte en dum ide!
När du logaritmerar VL kan du inte dela upp termerna. Du måste logaritmera hela VL tillsammans.
Med det sagt, e^4x är ju samma sak som (e^2x)^2. Testa substitutionen t=e^2x och se om det blir enklare att lösa.
Ok, då tolkar jag det som att substituering är det som krävs för att lösa uppgiften. Har för mig man löst liknande problem utan substituering. Men det är väl den 6:an som strular till det.
Volens27 skrev:Ok, då tolkar jag det som att substituering är det som krävs för att lösa uppgiften. Har för mig man löst liknande problem utan substituering. Men det är väl den 6:an som strular till det.
Ja börjar man nysta i det ser man att det inte trillar ut någon enkel lösning särskilt smidigt.
Man kan tänka sig att man flyttar 6:an till höger och börjar göra om vänsterledet i följande steg
e^4x + e^2x
e^2x ( e^2x + 1 )
... och applicerar ln[...] på båda sidor...
ln[ e^2x ( e^2x + 1 ) ]
ln[ e^2x ] + ln[ e^2x + 1 ]
... men här ser vi att även om första delen trillar ut lite enklare så är andra delen fortfarande knepig
2x + ln[ e^2x + 1 ]
Så även om pq-varianten känns omständig från början så är det nog snabbaste vägen mot målet.


