Exponentiella stokastiska variabler, sannolikhetslära

Jag har uppgiften:

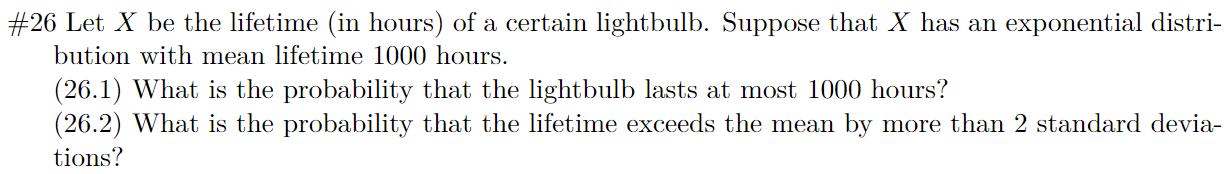
Eftersom det är en exponentiell fördelning så använder jag I 26.1 ska jag beräkna att den minst håller 1000 timmar, så jag tänker att detta ger $P (X \leq 1000)$ , som sökt. Med $λ = \frac{1}{μ} \Rightarrow λ = \frac{1}{1000}$ får jag $\int_{0}^{1000} λ e^{- λ x} d x = . . . = 1 - e^{- 1}$ .

Anledningen till att jag skriver att det är lika med F(1000) är att jag tänker det som ytan under grafen är det sökta, om hela ytan är lika med 1. Enligt bilden med x=1000:

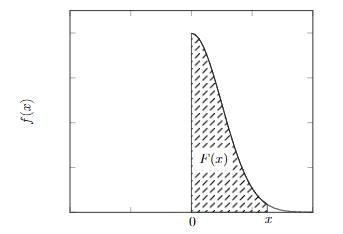
Stämmer det att man ska göra så?

Och i 26.2 undrar jag över hur man kommer fram till standardfördelningen?

X, brinntiden, är alltså exponentialfördelad. Det är en kontinuerlig fördelning.

Sannolikheten för att en lampa brinner i minst 1000 timmar blir väl P( X ≥ 1000) ?
Och P( X ≥ 1000) = P( X > 1000) eftersom det är en kontinuerlig fördelning,
så P( X ≥ 1000) = 1 – P( X ≤ 1000) = 1/e om du har räknat rätt ovan.
Visst?

Standardavvikelsen beräknar du via den vanliga beräkningsformeln för variansen.
Är du bekant med den?

Svara