Extrempunkt
Hejsan allihopa, tänkte kolla om något kan besvara mina funderingar. Har precis lät igenom hela derivatan i 3b och skall nu sätta mina kunskaper på prov, det känns tungt att de tog emot redan på andra frågan dock, men här är mina tankar kring det hela.
extrempunkt är vad jag förstår aningen där k=0 alltså i en minimipunkt eller maximipunkt, Eller när funktionen skär x axeln, dvs att om min teori stämmer så finns framför oss 3 extrempunkter. därav två i y = 0 och en i y=-4?
Så om detta är korrekt så skall man hitta bara en extrempunkt skulle i sådana fall detta vara minimipunkten i (-1,-4)?
Sen blir jag lite förvirrad där dom visar grafen till prim, alltså inte funktionen. Om detta ställer till något i mina tankar är oklara. SÅ slutfrågan är då , är det lättare än jag tror, är det bara koordinaterna till minimipunkten dom söker ? Tack på förhand !
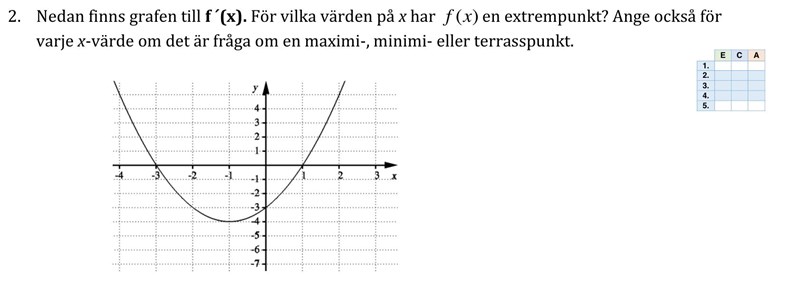
Kurvan visar funktionen f(x)s derivata. Frågan är när f(x) har extrempunkter.
Det infaller där derivatan är 0. Derivatans nollställen är där y värdet är noll, dvs där kurvan skär x axeln.
Kan du med denna ledning komma vidare?
philipk skrev:
extrempunkt är vad jag förstår aningen där k=0 alltså i en minimipunkt eller maximipunkt, Eller när funktionen skär x axeln, dvs att om min teori stämmer så finns framför oss 3 extrempunkter. därav två i y = 0 och en i y=-4?
Så om detta är korrekt så skall man hitta bara en extrempunkt skulle i sådana fall detta vara minimipunkten i (-1,-4)?
Sen blir jag lite förvirrad där dom visar grafen till prim, alltså inte funktionen. Om detta ställer till något i mina tankar är oklara. SÅ slutfrågan är då , är det lättare än jag tror, är det bara koordinaterna till minimipunkten dom söker ? Tack på förhand !
En extrempunkt kan som du skriver vara en maximum-, minimum-, terasspunkt eller en ändpunkt(dvs. Ändvärdet ifall funktionen bara är definierat inom ett visst område). Om du har en max, min eller terasspunkt så kommer lutningen i punkten vara noll(tangenten är horisontell). Så grafen de ritat, f'(x) som är derivatan av f(x), visar dessa punkter då f'(x)=0 alltså skär x-axeln. För att bestämma o det är en max min eller terasspunkt så får du kolla på vad som händer med derivatans tecken kring punkten. Hur ändras lutningen kring en max-punkt? Hur ändras lutningen kring en min-punkt resp. Terass-punkt?
Ture skrev:Kurvan visar funktionen f(x)s derivata. Frågan är när f(x) har extrempunkter.
Det infaller där derivatan är 0. Derivatans nollställen är där y värdet är noll, dvs där kurvan skär x axeln.
Kan du med denna ledning komma vidare?
Nje nu förstår jag inte riktigt, genom att ställa upp f′(x)=0 alltså 0 betyder där lutningen är noll i derivata, det är ju vid maximi eller minimi punkten? Du menar att dervatans nollställe ärr där y värdet är noll, dvs att de dom söker är där kurvan skär x alltså -3,0 och 1,0? Med vänlig hälsning,
Engineering skrev:philipk skrev:
extrempunkt är vad jag förstår aningen där k=0 alltså i en minimipunkt eller maximipunkt, Eller när funktionen skär x axeln, dvs att om min teori stämmer så finns framför oss 3 extrempunkter. därav två i y = 0 och en i y=-4?
Så om detta är korrekt så skall man hitta bara en extrempunkt skulle i sådana fall detta vara minimipunkten i (-1,-4)?
Sen blir jag lite förvirrad där dom visar grafen till prim, alltså inte funktionen. Om detta ställer till något i mina tankar är oklara. SÅ slutfrågan är då , är det lättare än jag tror, är det bara koordinaterna till minimipunkten dom söker ? Tack på förhand !En extrempunkt kan som du skriver vara en maximum-, minimum-, terasspunkt eller en ändpunkt(dvs. Ändvärdet ifall funktionen bara är definierat inom ett visst område). Om du har en max, min eller terasspunkt så kommer lutningen i punkten vara noll(tangenten är horisontell). Så grafen de ritat, f'(x) som är derivatan av f(x), visar dessa punkter då f'(x)=0 alltså skär x-axeln. För att bestämma o det är en max min eller terasspunkt så får du kolla på vad som händer med derivatans tecken kring punkten. Hur ändras lutningen kring en max-punkt? Hur ändras lutningen kring en min-punkt resp. Terass-punkt?
Fantastiskt förklarat! Fick läsa några gånger för att vara säker på vad du sa men om jag förstår det hela rätt så är det när f′ grafen skär x, dvs de är där f′(x)=0 , att lutningen är noll, och nästa steg är att förstå som du skrev vilken typ det handlar om, alltså om det är en maximipunkt, minimipunkt eller Terass i koordinat (-3,0) alltså till vänster om y axeln och koordinat (1,0) till höger om y axeln. Och då ska man kolla vilka tecken? Jag måste nog klura lite på de sista bara!
philipk skrev:Ture skrev:Kurvan visar funktionen f(x)s derivata. Frågan är när f(x) har extrempunkter.
Det infaller där derivatan är 0. Derivatans nollställen är där y värdet är noll, dvs där kurvan skär x axeln.
Kan du med denna ledning komma vidare?
Nje nu förstår jag inte riktigt, genom att ställa upp f′(x)=0 alltså 0 betyder där lutningen är noll i derivata, det är ju vid maximi eller minimi punkten? Du menar att dervatans nollställe ärr där y värdet är noll, dvs att de dom söker är där kurvan skär x alltså -3,0 och 1,0? Med vänlig hälsning,
Ja exakt, funktionen f(x) har extrempunkter när f'(x) skär x-axeln. För då är f'(x)=0 och lutningen för f(x)=0
Min tanke om f′(x) grafen när det kommer till lutningen, vid y=0 innebär att k =0 . Sedan går ju grafen ner mot ett negativt y värde efter först (-3,0) , då går den från en maximipunkt sen avtar lutingen fram till (1.0) sen blir + dvs att andra är minimi? kan detta stämma??
Engineering skrev:philipk skrev:Ture skrev:Kurvan visar funktionen f(x)s derivata. Frågan är när f(x) har extrempunkter.
Det infaller där derivatan är 0. Derivatans nollställen är där y värdet är noll, dvs där kurvan skär x axeln.
Kan du med denna ledning komma vidare?
Nje nu förstår jag inte riktigt, genom att ställa upp f′(x)=0 alltså 0 betyder där lutningen är noll i derivata, det är ju vid maximi eller minimi punkten? Du menar att dervatans nollställe ärr där y värdet är noll, dvs att de dom söker är där kurvan skär x alltså -3,0 och 1,0? Med vänlig hälsning,
Ja exakt, funktionen f(x) har extrempunkter när f'(x) skär x-axeln. För då är f'(x)=0 och lutningen för f(x)=0
Intressant! Men kan du se över min andra fråga som jag inte citerade dig men ligger strax under, hoppas min förståelse är korrekt i sådana fall så förstår jag alltihopa och släppa min ångest och ta på min lyckokoftan igen xD
philipk skrev:Min tanke om f′(x) grafen när det kommer till lutningen, vid y=0 innebär att k =0 . Sedan går ju grafen ner mot ett negativt y värde efter först (-3,0) , då går den från en maximipunkt sen avtar lutingen fram till (1.0) sen blir + dvs att andra är minimi? kan detta stämma??
Ja precis det stämmer. Om f'(x) hade haft sitt minimum vid x-axeln, dvs. Aldrig skurit ned till negativt värde så hade det varit en terasspunkt eftersom värdet gått från positivt och sedan till 0 och sedan positivt igen. Samma sak gäller såklart om det går feån negativt till 0 och negativt igen
Engineering skrev:philipk skrev:Min tanke om f′(x) grafen när det kommer till lutningen, vid y=0 innebär att k =0 . Sedan går ju grafen ner mot ett negativt y värde efter först (-3,0) , då går den från en maximipunkt sen avtar lutingen fram till (1.0) sen blir + dvs att andra är minimi? kan detta stämma??
Ja precis det stämmer. Om f'(x) hade haft sitt minimum vid x-axeln, dvs. Aldrig skurit ned till negativt värde så hade det varit en terasspunkt eftersom värdet gått från positivt och sedan till 0 och sedan positivt igen. Samma sak gäller såklart om det går feån negativt till 0 och negativt igen
wow stort tack , detta var grym info. på återseende ;P
philipk skrev:Engineering skrev:philipk skrev:Min tanke om f′(x) grafen när det kommer till lutningen, vid y=0 innebär att k =0 . Sedan går ju grafen ner mot ett negativt y värde efter först (-3,0) , då går den från en maximipunkt sen avtar lutingen fram till (1.0) sen blir + dvs att andra är minimi? kan detta stämma??
Ja precis det stämmer. Om f'(x) hade haft sitt minimum vid x-axeln, dvs. Aldrig skurit ned till negativt värde så hade det varit en terasspunkt eftersom värdet gått från positivt och sedan till 0 och sedan positivt igen. Samma sak gäller såklart om det går feån negativt till 0 och negativt igen
wow stort tack , detta var grym info. på återseende ;P
Som extra tips så brukar man kolla på andra derivatan för att bestämma max eller minpunkt. Om andraderivatan är negativ (f'(x) har negativ lutning) så är det en maxpunkt och tvärt om vid positiv andraderivata.
LÖSTE FRÅGAN! Med din metod #Engineering, grymt! det kändes ju toppen! :)
Tog bort dina skrikiga versaler från rubriken. De står i Pluggakutens regler (och ovanför rutan där man skriver in sin rubrik) att man skall undvika att skriva rubriken med bara stora bokstäver. /moderator
