Extremvärde
Uppgiften är att man ska bestämma om funktionen har lokala eller absolute extreme values ( antar de menar ändpunkterna)
Uppgift :
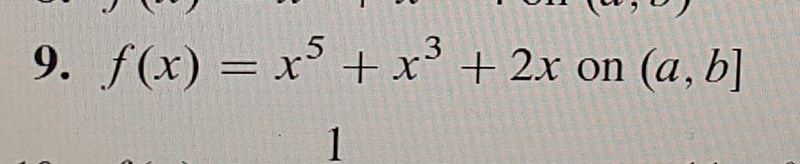 facit:
facit:
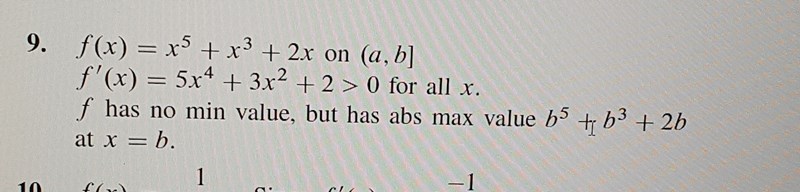
För att vi har en mjuk parantes så a ingår inte intervallet. Men hur vet man det inte finns några andra värde mellan a till b som kan ge en minimi punkt? Och också hur vet man att b ger maximi punkten ??
Vi har inga kritiska punkter och vi har även inga singulära punkter och vi har en ändpunkt som är x=b.
Eftersom f’ är positiv överallt så växer f överallt. Tänk dig själv, en ständig uppförsbacke, var skulle den ha minimum eller maximum? Det kan bara vara i ändpunkterna. Men vänstra ändpunkten finns inte med i grafen, bara den högra, och där är det globalt (och lokalt förstås) maximum.
“Det gick inte att derivera…”, hurdå, det går väl hur lätt som helst?
Mogens skrev:“Det gick inte att derivera…”, hurdå, det går väl hur lätt som helst?
Sorry jag menade det har inga kritiska punkter. Alltså f' =0
Mogens skrev:Eftersom f’ är positiv överallt så växer f överallt. Tänk dig själv, en ständig uppförsbacke, var skulle den ha minimum eller maximum? Det kan bara vara i ändpunkterna. Men vänstra ändpunkten finns inte med i grafen, bara den högra, och där är det globalt (och lokalt förstås) maximum.
OK, så a och b är positiva.
Tack så mycket för att du svarade så snabb!! Nu när jag har förstått så kan jag gå vidare till andra uppgifter!!:))
Nejnej, varken a eller b måste vara positiva.
Hahah ja du har rätt. Är trött och såg inte att har x^4 och x^2 så f' kommer alltid att vara positiv.

