f(x)=asin(kx)+dx
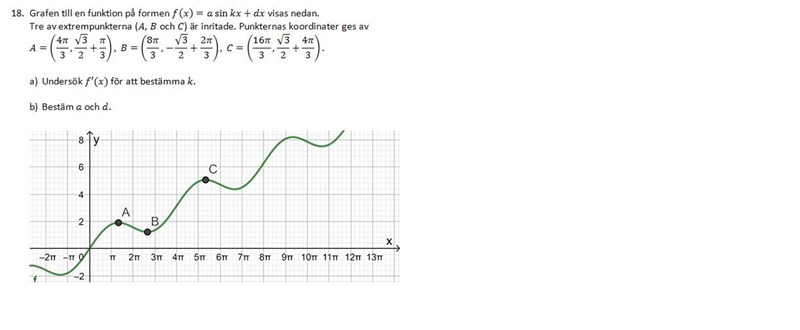
Först har jag deriverat f(x) 0ch undersökt att k måste lika med 0
f(x)=asin(kx)+dx
a) f`(x)=ak cos(k x)+ d
0 =ak cos(4pi/3)k+ d..........(1)
0 =ak cos(8pi/3)k+ d..........(2)
0 =ak cos(16pi/3)k+ d......(3)
k=0
b) (rot(3)/2) + pi/3= a sin(4pi/3)k+ (4pi/3)d............1
(-rot(3)/2) + 2pi/3= a sin(8pi/3)k+ (8pi/3)d.........2
(rot(3)/2) + 4pi/3= a sin(16pi/3)k+ (16pi/3)d.......3
Nu är jag tveksam att lösa de 3 ekv. eftersom har jag fåttt från a svaret att k=0 och undrar om det finns enklare tanke at göra
Dra en rät linje mellan A och C. Lutningen på en linjen är lika med d.
Periodtiden på sin() läses på x-axeln som skillnaden mellan C och A
När k och d är kända kan man ta vilket x-värde som helst för att beräkna a
jag fått medwllande från lärare att k det inte blir noll, nu jag vill säga att jag inte kan lösa problemet. Den första delen (a) f`(x) och tre ekv.kan inte lösa
Affe Jkpg skrev:Dra en rät linje mellan A och C. Lutningen på en linjen är lika med d.
Periodtiden på sin() läses på x-axeln som skillnaden mellan C och A
När k och d är kända kan man ta vilket x-värde som helst för att beräkna a
Periodtiden på sin() läses på x-axeln som skillnaden mellan C och A
Om man nu nödvändigtvis ska behöva skriva något om f´(x)
a) f´(x)=0 i punkterna A, B och C, men avståndet på x-axeln mellan A och C motsvarar en hel period (). Periodtiden för f(x) och f'(x) är samma, så:
Om k= 1/2 a= -1 d= 1/4
f(x)= -sin(1/2x)+1/4x
men när jag den f kommer det inte samma graf
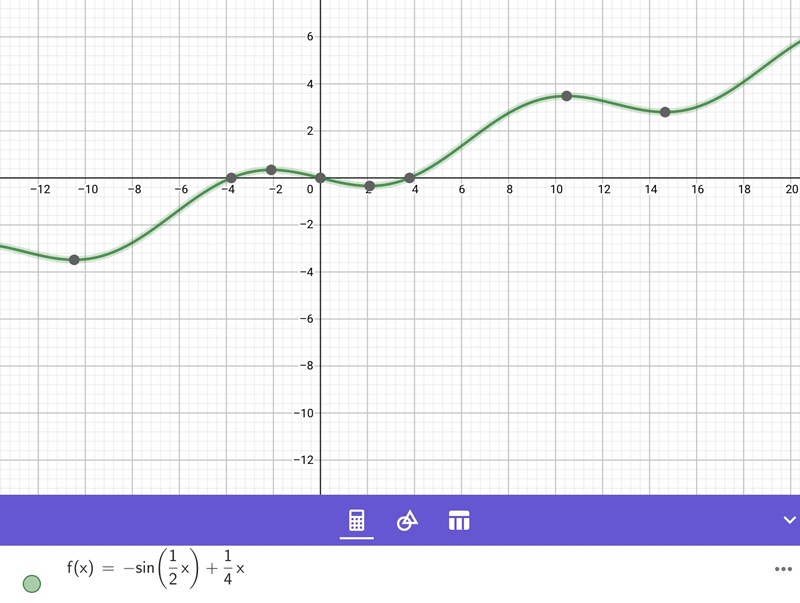
d ska inte vara 1/4. Hur fick du det?
Affe Jkpg skrev:Dra en rät linje mellan A och C. Lutningen på en linjen är lika med d.
Periodtiden på sin() läses på x-axeln som skillnaden mellan C och A
När k och d är kända kan man ta vilket x-värde som helst för att beräkna a
Dra en rät linje mellan A och C. Lutningen på den linjen är lika med d.
I punkterna A och C gäller för 2: minus 1:
Nu har jag löst a= 1 d = 1/4 k= 1/2 trots att jag inte kunde lösa de tre f`(x) =0 ekv. För att lösa k= 1/2
Om man tänker på vad har jag lärt mig i matematik måste jag lösa de tre f'(x) ekv . Men jag är ledsen.
visa din lösning jag mistänker att du gjort fel någonstans.
Hej!
Om eller om så blir funktionen och figuren visar att grafen inte är en rät linje; därför måste det gälla att och att .
I de två punkterna och är funktionens derivata lika med noll.
Subtrahera de två ekvationerna för att bli av med konstanten .
där jag infört beteckningen Varken eller är lika med noll så den enda möjligheten är att och additionssats för cosinusfunktionen ger andragradsekvationen
Följande figur visar grafen till funktionen ; bilden liknar den i uppgiftstexten, vilket indikerar att ligger i närheten av och att ligger i närheten av .
Det går att beräkna exakta värden på både och .
Affe Jkpg skrev:Dra en rät linje mellan A och C. Lutningen på en linjen är lika med d.
Periodtiden på sin() läses på x-axeln som skillnaden mellan C och A
När k och d är kända kan man ta vilket x-värde som helst för att beräkna a
När d är känt kan man ta lämpligt x-värde för att beräkna a
Vi tar värden i punkten A.
eftersom



