f´(x) parallell med rät linje

Hej.

Kan inte förstå en sak i följande uppgift:

Uppgift:

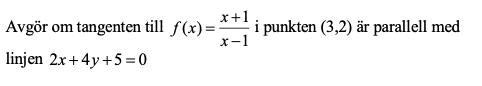
Egna tankar

Nedan ser ni två bilder. Den första är min lösning. Den andra är f´(3). Det som jag tycker är knäppt här är att i min grafräknare ger f´(3) ett positivt värde=1/2. Medan jag i min uträkning får lutningen i punkten till samma värde fast negativt: -1/2. Hur kommer det sig att dessa skiljer sig åt? Varför detta bekymrar mig är för att jag vill kunna "dubbelkontrollera" mina svar grafiskt i räknaren. Som alltid tack för den tid ni tar till att hjälpa till!

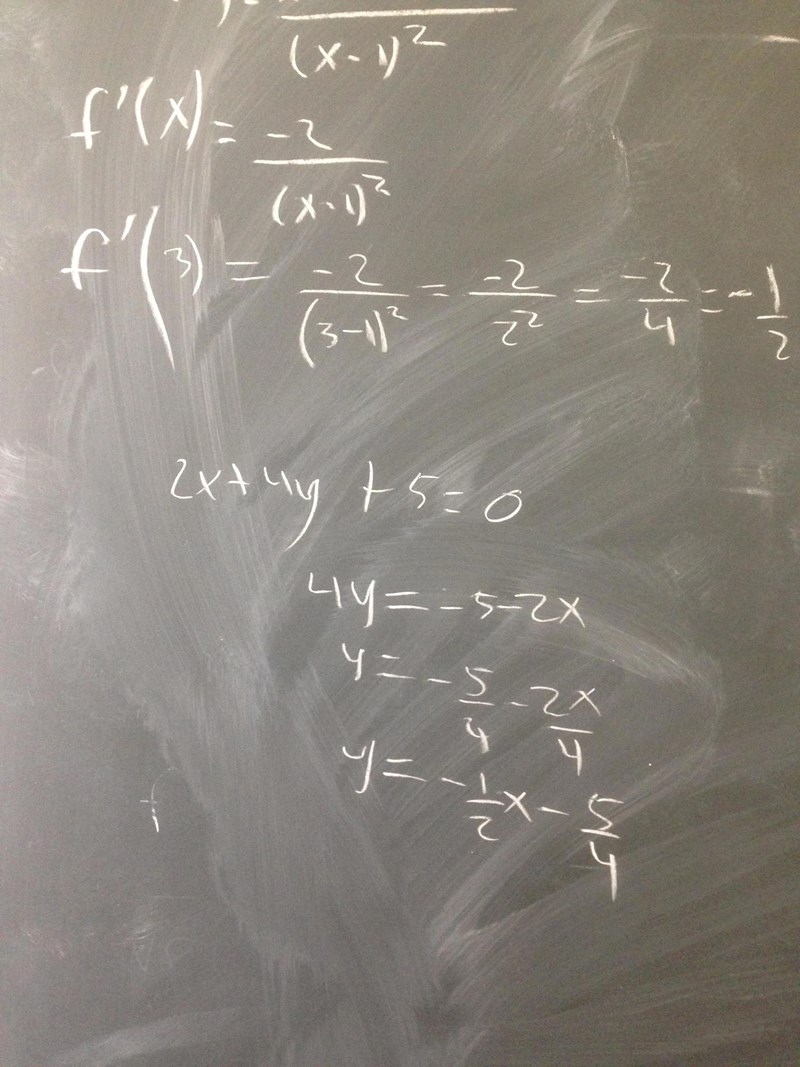
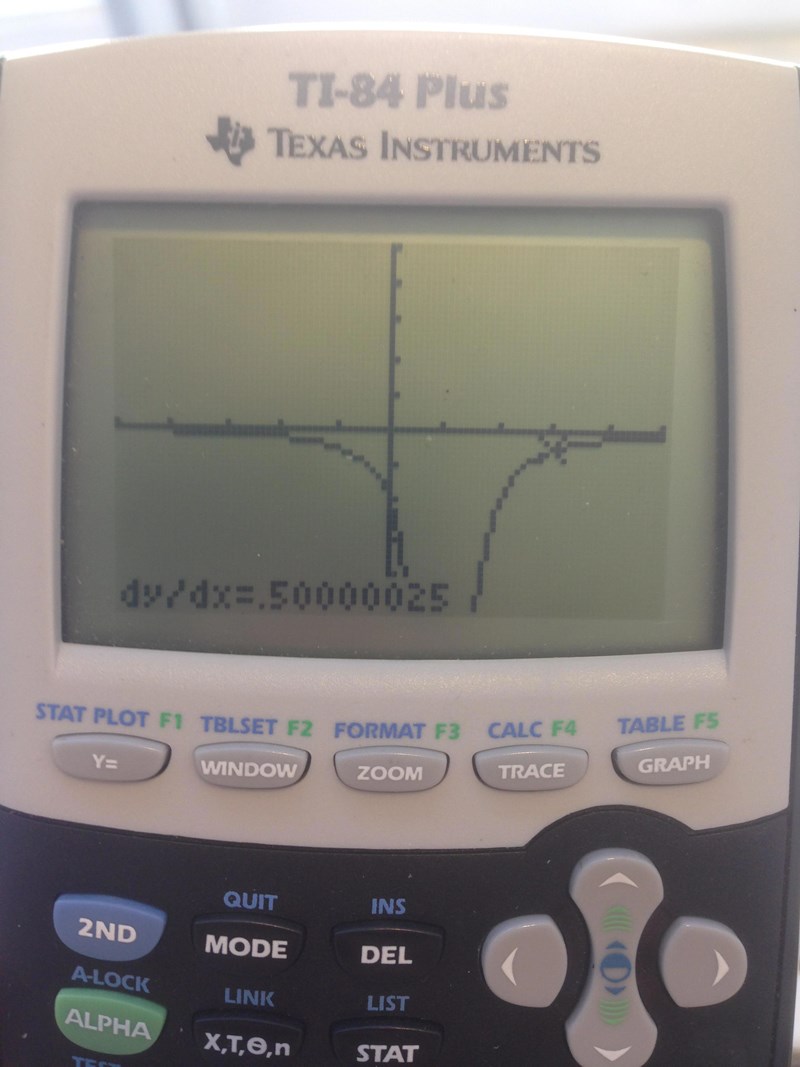
Du har inte ritat in rätt graf, kontrollera igen.

Det gäller nämligen att:

$\lim_{x \to 1^-}\frac{x+1}{x-1}=-\infty$

och

$\lim_{x\to 1^+}\frac{x+1}{x-1}=\infty$

Vad du har gjort är att du har ritat upp derivatan på din miniräknare och sedan beräknat derivatans derivata, d.v.s. andraderivatan i punkten $x=3$ .

Vad du ska göra är att rita in den ursprungliga funktionen och sedan gå på 2nd CALC och räkna ut derivatan.

Det verkar som att du plottat förstaderivatan: $f'(x)$ . Det innebär att om du sedan läser av $\frac{dy}{dx}$ av den så blir det i själva verket andraderivatan.

Tack för snabba svar ni är super nu förstår jag!

Svara

Visa senaste svar